题目内容
3.宇航员站在一星球表面上,以水平速度V0抛出一小球,抛出点离地高度为h.测得落地点与抛出点间的水平距离为L,已知该星球的半径为R,万有引力常量为G.求:该星球的质量M.分析 根据平抛运动的规律求出星球表面的重力加速度,结合万有引力等于重力求出星球的质量.
解答 解:设该星球表面的重力加速度为g,据平抛运动公式:
水平方向L=V0t------------①
竖直方向h=$\frac{1}{2}$gt2----------②
整理①②得:g=$\frac{2{hv}_{0}^{2}}{{L}^{2}}$
根据万有引力等于重力,
$\frac{GMm}{{R}^{2}}$=mg
$M=\frac{{2hV_0^2{R^2}}}{{G{L^2}}}$
答:该星球的质量是$M=\frac{{2hV_0^2{R^2}}}{{G{L^2}}}$.
点评 解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律,以及掌握万有引力等于重力这一理论,并能灵活运用.

练习册系列答案
相关题目
11.关于功率,以下说法不正确的是( )
| A. | 单位时间内物体做功越多,其功率越大 | |
| B. | 物体做功越多,它的功率就越大 | |
| C. | 物体做功越快,它的功率就越大 | |
| D. | 额定功率是发动机正常工作时的最大输出功率 |
8.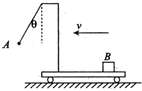 如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )
如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )
 如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )
如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )| A. | mg,竖直向上 | B. | mg$\sqrt{1+{μ}^{2}}$,斜向左上方 | ||
| C. | mgtanθ,水平向右 | D. | mg$\sqrt{1+ta{n}^{2}θ}$,斜向右上方 |
15. 如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}$=2$\overline{PO}$,则两小球质量之比m1:m2为( )
如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}$=2$\overline{PO}$,则两小球质量之比m1:m2为( )
 如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}$=2$\overline{PO}$,则两小球质量之比m1:m2为( )
如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}$=2$\overline{PO}$,则两小球质量之比m1:m2为( )| A. | 7:5 | B. | 4:3 | C. | 2:1 | D. | 5:3 |
12.对于万有引力定律的数学表达式F=G$\frac{Mm}{{r}^{2}}$,下列说法正确的是( )
| A. | 公式中G为万有引力常量,是人为规定的,可以取不同的值 | |
| B. | r趋近于零时,万有引力趋于无穷大 | |
| C. | 公式适用于可视为质点的两物体间引力的计算 | |
| D. | M、m之间的万有引力总是大小相等方向相反,是一对相互作用力 |
 一半径为r的圆形导线框内有一匀强磁场,磁场方向垂直于导线框所在平面,导线框的左端通过导线接一对水平放置的平行金属板,两板间的距离为d,磁场的磁感应强度B随时间t均匀增大且关系式为:B=kt+B0开始,磁感应强度的变化率为k,在平行板内有一质量为m的带电液滴静止于两板中间,该液滴可视为质点,重力加速度为g.
一半径为r的圆形导线框内有一匀强磁场,磁场方向垂直于导线框所在平面,导线框的左端通过导线接一对水平放置的平行金属板,两板间的距离为d,磁场的磁感应强度B随时间t均匀增大且关系式为:B=kt+B0开始,磁感应强度的变化率为k,在平行板内有一质量为m的带电液滴静止于两板中间,该液滴可视为质点,重力加速度为g. 如图所示,一物块在水平恒力F=6N的作用下从A点由静止开始沿水平直轨道运动到B点,物块飞出后越过“壕沟”落在平台EG段,已知物块的质量m=1kg,物块与水平直轨道间的动摩擦因数为μ=0.4,AB段长L=9m,BE的高度差h=0.8m,BE的水平距离x=1.6m,若物块可看做质点,空气阻力不计,g取10m/s2.求:
如图所示,一物块在水平恒力F=6N的作用下从A点由静止开始沿水平直轨道运动到B点,物块飞出后越过“壕沟”落在平台EG段,已知物块的质量m=1kg,物块与水平直轨道间的动摩擦因数为μ=0.4,AB段长L=9m,BE的高度差h=0.8m,BE的水平距离x=1.6m,若物块可看做质点,空气阻力不计,g取10m/s2.求: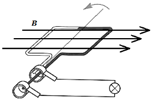 一个小型应急交流发电机.内部为n=50匝边长L=20cm的正方形线圈,总电阻为r=1.0Ω.线圈在磁感应强度为B=0.1T的匀强磁场中,绕垂直于磁感线的轴匀速转动.发电机对一电阻为R=9.0Ω的电灯供电,线路中其它电阻不计,若发电机的转动角速度为ω=100rad/s时,电灯正常发光.求:
一个小型应急交流发电机.内部为n=50匝边长L=20cm的正方形线圈,总电阻为r=1.0Ω.线圈在磁感应强度为B=0.1T的匀强磁场中,绕垂直于磁感线的轴匀速转动.发电机对一电阻为R=9.0Ω的电灯供电,线路中其它电阻不计,若发电机的转动角速度为ω=100rad/s时,电灯正常发光.求: