题目内容
如图1所示，在倾角α=60°的斜面上放一个质量m的物体，用k=100N/m的轻弹簧平行斜面吊着．发现物体放在PQ间任何位置恰好都处于静止状态，测得AP=22cm，AQ=8cm，则物体与斜面间的最大静摩擦力等于多少？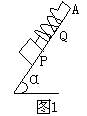
解析:
物体位于Q点时，弹簧必处于压缩状态，对物体的弹簧TQ沿斜面向下；物体位于P点时，弹簧已处于拉伸状态，对物体的弹力Tp沿斜面向上．P，Q两点是物体静止于斜面上的临界位置，此时斜面对物体的静摩擦力都达到最大值fm，其方向分别沿斜面向下和向上．
【解】 作出物体在P、Q两位置时的受力图（图2），设弹簧原长为L0，则物体在Q和P两处的压缩量和伸长量分别为
x1=L0-AQ，x2=AP-L0．
根据胡克定律和物体沿斜面方向的力平衡条件可知：
kx1 =k（L0-AQ）=fm - mgsinα，
kx2 =k（AP-L0）=fm + mgsinα．
联立两式得
【说明】 题中最大静摩擦力就是根据物体的平衡条件确定的，所以画出P、Q两位置上物体的受力图是至关重要的．
练习册系列答案
相关题目
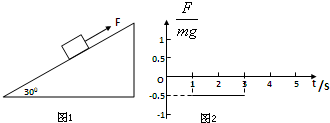（2010?嘉定区一模）如图1所示，在倾角为30°的足够长的光滑斜面上有一质量为m=1kg的物体，它受到沿斜面方向的力F的作用．力F按图2变化（图中纵坐标是力F与mg的比值，力F沿斜面向上为正）．已知此物体在t=0时速度为零，那么此物体在4s末的速率为
