题目内容
如图1所示,在倾角为α的斜面上,放一质量为m的小球,小球被竖直的木板挡住,不计摩擦,则球对挡板的压力是( )?
图1
A.mgcosα B.mgtanα
C.mgcosα D.mg
解析:解法一(正交分解法):对小球受力分析如图2所示,小球静止,处于平衡状态,沿水平和竖直方向建立坐标系,将N2正交分解,列平衡方程为 N1=N2sinα mg=N2cosα
可得:球对挡板的压力N1′=N1=mgtanα,所以B正确.

图2
解法二(力的合成法):如图3所示,小球处于平衡状态,合力为零.N1与N2的合力一定与mg平衡,即等大反向.解三角形可得:N1=mgtanα,所以,球对挡板的压力N1′=N1=mgtanα.所以B正确.

图3
解法三(力的分解法):如图4所示,小球的重力mg的两个分力与N1、N2大小相等、方向相反,故N1=mgtanα,球对挡板的压力N1′=N1=mgtanα.所以B正确.

图4
解法四(三角形法则):如图5所示,小球处于平衡状态,合力为零,所受三个力经平移首尾顺次相接,一定能构成封闭三角形.由三角形解得:N1=mgtanα,故挡板受压力N1′=N1=mgtanα.所以B正确.

图5
答案:B

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
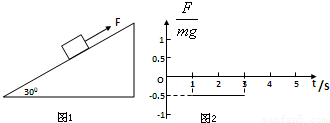
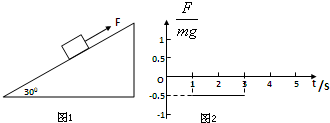 (2010?嘉定区一模)如图1所示,在倾角为30°的足够长的光滑斜面上有一质量为m=1kg的物体,它受到沿斜面方向的力F的作用.力F按图2变化(图中纵坐标是力F与mg的比值,力F沿斜面向上为正).已知此物体在t=0时速度为零,那么此物体在4s末的速率为
(2010?嘉定区一模)如图1所示,在倾角为30°的足够长的光滑斜面上有一质量为m=1kg的物体,它受到沿斜面方向的力F的作用.力F按图2变化(图中纵坐标是力F与mg的比值,力F沿斜面向上为正).已知此物体在t=0时速度为零,那么此物体在4s末的速率为