题目内容
14. 如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=2kg的无人机,其动力系统所能提供的最大升力F=36N,运动过程中所受空气阻力大小恒为f=4N.g取10m/s2.
如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=2kg的无人机,其动力系统所能提供的最大升力F=36N,运动过程中所受空气阻力大小恒为f=4N.g取10m/s2.(1)无人机在地面上从静止开始,以最大升力竖直向上起飞.求在t=5s时离地面的高度h;
(2)当无人机悬停在距离地面高度H=100m处,由于动力设备故障,无人机突然失去升力而坠落.求无人机坠落地面时的速度v;
(3)在无人机坠落过程中,在遥控设备的干预下,动力设备重新启动提供向上最大升力.为保证安全着地,求飞行器从开始下落到恢复升力的最长时间t1.
分析 (1)根据牛顿第二定律求出上升的加速度,结合位移时间公式求出上升的位移.
(2)根据牛顿第二定律求出下降的加速度大小,结合速度位移公式求出坠落地面时的速度大小.
(3)根据牛顿第二定律求出恢复升力后向下减速的加速度,抓住匀加速和匀减速运动的位移之和等于H,求出最大速度,结合速度时间公式求出飞行器从开始下落到恢复升力的最长时间t1.
解答 解:(1)由牛顿第二定律 F-mg-f=ma
代入数据解得a=6m/s2
上升高度 $h=\frac{1}{2}a{t^2}$
代入数据解得 h=75m.
(2)下落过程中 mg-f=ma1
代入数据解得${a_1}=8m/{s^2}$
落地时速度 v2=2a1H,
代入数据解得 v=40m/s
(3)恢复升力后向下减速运动过程 F-mg+f=ma2
代入数据解得${a_2}=10m/{s^2}$
设恢复升力时的速度为vm,则有 $\frac{{{v_m}^2}}{{2{a_1}}}+\frac{{{v_m}^2}}{{2{a_2}}}=H$
${v_m}=\frac{{40\sqrt{5}}}{3}m/s$
由 vm=a1t1
代入数据解得 ${t_1}=\frac{{5\sqrt{5}}}{3}s$.
答:(1)t=5s时离地面的高度h为75m.
(2)无人机坠落地面时的速度为40m/s.
(3)飞行器从开始下落到恢复升力的最长时间为$\frac{5\sqrt{5}}{3}s$.
点评 本题的关键是对飞行器的受力分析以及运动情况的分析,结合牛顿第二定律和运动学基本公式求解,本题难度适中.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
2.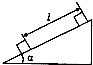 如图所示,质量为m的物体从静止开始沿倾角为α的粗糙固定斜面下滑了一段距离l,物体与斜面间的动摩擦因数为μ,下列说法正确的是( )
如图所示,质量为m的物体从静止开始沿倾角为α的粗糙固定斜面下滑了一段距离l,物体与斜面间的动摩擦因数为μ,下列说法正确的是( )
 如图所示,质量为m的物体从静止开始沿倾角为α的粗糙固定斜面下滑了一段距离l,物体与斜面间的动摩擦因数为μ,下列说法正确的是( )
如图所示,质量为m的物体从静止开始沿倾角为α的粗糙固定斜面下滑了一段距离l,物体与斜面间的动摩擦因数为μ,下列说法正确的是( )| A. | 重力对物体做功为mgl | |
| B. | 物体下滑距离l,机械能损失了μmgl | |
| C. | 物体受3个力作用,3个力做的总功为W=mgl(sinα-μcosα) | |
| D. | 物体下滑距离l时,重力对物体做功的瞬时功率为mg$\sqrt{2(gsinα-μgcosα)l}$ |
3.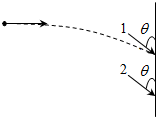 某同学前后两次从同一位置水平投出两支飞镖1和飞镖2到靶盘上,飞镖落到靶盘上的位置如图所示,忽略空气阻力,则两支飞镖在飞行过程中( )
某同学前后两次从同一位置水平投出两支飞镖1和飞镖2到靶盘上,飞镖落到靶盘上的位置如图所示,忽略空气阻力,则两支飞镖在飞行过程中( )
 某同学前后两次从同一位置水平投出两支飞镖1和飞镖2到靶盘上,飞镖落到靶盘上的位置如图所示,忽略空气阻力,则两支飞镖在飞行过程中( )
某同学前后两次从同一位置水平投出两支飞镖1和飞镖2到靶盘上,飞镖落到靶盘上的位置如图所示,忽略空气阻力,则两支飞镖在飞行过程中( )| A. | 加速度a1>a2 | B. | 飞行时间t1<t2 | C. | 初速度v1=v2 | D. | 角度θ1=θ2 |
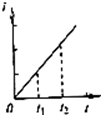
4.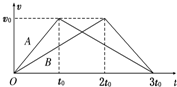 质量分别为2m和m的A、B两种物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其v t图象如图所示,则下列说法正确的是( )
质量分别为2m和m的A、B两种物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其v t图象如图所示,则下列说法正确的是( )
 质量分别为2m和m的A、B两种物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其v t图象如图所示,则下列说法正确的是( )
质量分别为2m和m的A、B两种物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其v t图象如图所示,则下列说法正确的是( )| A. | F1等于4F2 | |
| B. | F1、F2对A、B做功之比为2:1 | |
| C. | A受到的摩擦力大于B受摩擦力 | |
| D. | 全过程中摩擦力对A、B做功之比为1:1 |
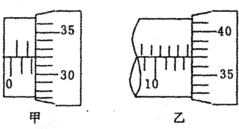 在“双缝干涉测量光的波长实验”中;
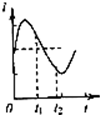
在“双缝干涉测量光的波长实验”中;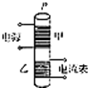 如图所示,在铁芯P上绕着两个线圈甲和乙.如果线圈中的电流i与时间t的变化有下面A,B,C,D四种情况,在t1至t2这段时间内,哪种情况可以观察到在线圈乙中有交变电流.( )
如图所示,在铁芯P上绕着两个线圈甲和乙.如果线圈中的电流i与时间t的变化有下面A,B,C,D四种情况,在t1至t2这段时间内,哪种情况可以观察到在线圈乙中有交变电流.( )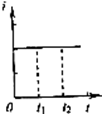

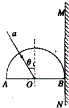 如图所示,半圆玻璃砖的半径R=20cm,直径AB与屏幕垂直并接触于B点,玻璃砖的折射率n=$\sqrt{2}$,激光束α以入射角θ1=30°射向半圆玻璃砖的圆心O,结果在屏幕MN上出现两个光斑.(结果保留两位有效数字)求:
如图所示,半圆玻璃砖的半径R=20cm,直径AB与屏幕垂直并接触于B点,玻璃砖的折射率n=$\sqrt{2}$,激光束α以入射角θ1=30°射向半圆玻璃砖的圆心O,结果在屏幕MN上出现两个光斑.(结果保留两位有效数字)求: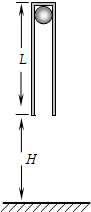 如图所示,一个质量为M=0.4kg,长为L的圆管竖直放置,顶端塞有一个质量为m=0.1kg的弹性小球,球和管间的滑动摩擦力和最大静摩擦力大小均为4N.管从下端离地面距离为H=0.8m处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起时的速度与刚要落地时速度大小相等,不计空气阻力,重力加速度为g=10m/s2.
如图所示,一个质量为M=0.4kg,长为L的圆管竖直放置,顶端塞有一个质量为m=0.1kg的弹性小球,球和管间的滑动摩擦力和最大静摩擦力大小均为4N.管从下端离地面距离为H=0.8m处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起时的速度与刚要落地时速度大小相等,不计空气阻力,重力加速度为g=10m/s2.