题目内容

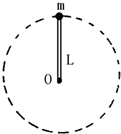
用长为L的轻质细杆拉着质量为m的小球在竖直平面内作圆周运动，小球运动到最高点时，速率等于2
gL
，不计空气阻力，求：
（1）小球在最高点所受力的大小和方向？
（2）小球运动到最低点时的速度大小是多少？

（1）假设小球在最高时，所受杆的弹力方向竖直向下，由牛顿第二定律得
mg+F=m
v2
L
，又v=2
gL
，
得到F=m
v2
L
-mg=3mg＞0，说明弹力的方向竖直向下．
（2）小球从最高点运动到最低点过程中，由机械能守恒定律得
2mgL+
1
2
mv2=
1
2
mv′2
代入解得：小球运动到最低点时的速度大小v′=2
2gL
．
答：（1）小球在最高点所受力的大小3mg，方向竖直向下；
（2）小球运动到最低点时的速度大小为2
2gL
．
练习册系列答案
相关题目
如图所示，将完全相同的两小球A、B，用长L=0.8m的细绳悬于以v=4m/s向左匀速运动的小车顶部，两球与小车前后壁接触．由于某种原因，小车突然停止，此时悬线中张力之比FB：FA为（g=10m/s2）（　　）
A．1：1B．1：2C．1：3D．1：4
一个滑雪人质量m=75㎏，以v0=2m/s的初速度沿山坡匀加速滑下，山坡的倾角θ=30°，在t=5s的时间内滑下的路程x=60m．
求：（1）滑雪人的加速度；
（2）求滑雪人受到的阻力（g取10m/s2）
如图所示，倾斜放置的圆盘绕着中轴匀速转动，圆盘的倾角为37°，在距转动中心r=0.1m处放一个小木块，小木块跟随圆盘一起转动，小木块与圆盘间的动摩擦因数为μ=0.8，假设木块与圆盘的最大静摩擦力与相同条件下的滑动摩擦力相同．若要保持小木块不相对圆盘滑动，圆盘转动的角速度最大不能超过（　　）
A．2rad/sB．8rad/sC．
124
rad/s		D．
60
rad/s
如图，小车在水平面上以4m/s的速度向右做匀速直线运动，车厢内用OA、OB两细绳系住一个质量为2kg的物体，OA与竖直方向夹角为θ=37°，OB是水平的．后来小车改做匀减速运动，经8m的位移停下来（运动过程OB拉力不为0）．
求：（1）车在匀速运动的过程中，两绳的拉力TA、TB各是多少？（sin37°=0.6）
（2）车在匀减速运动的过程中，两绳的拉力TA、TB各是多少？（g取10m/s2）
水平传送带匀速运动，速度大小为v，现将一个小工件（初速度为零）放到传送带上，它将在传送带上滑行一段时间后与传带保持相对静止．设工件质量为m，它与传送带间的动摩擦因数为μ，在这段相对滑行的过程中（　　）
A．滑动摩擦力对传送带做的功是-
1
2
mv2
B．工件的机械能增量是mv2
C．工件相对于传送带滑动的路程大小为
v2
2μg
D．工件与传送带相对滑动产生的热量是mv2
一平板车，质量M=100kg，停在水平路面上，车身的平板离地面的高度h=1.25m，一质量m=50kg的物块置于车的平板上，它到车尾端的距离b=1.00m，与车板间的动摩擦因数μ=0.20．如图所示．今对平板车施一水平方向的恒力使车向前行驶，结果物块从车板上滑落．物块刚离开车板的时刻，车向前行驶的距离s0=2.0m，求物块落地时，落地点到车尾的水平距离s．不计路面与平板车间以及轮轴之间的摩擦，取g=10m/s2．
水平传送带被广泛地应用于机场和火车站，便于对旅客的行李进行安全检查．图为一水平传送带装置示意图，绷紧的传送带A、B始终保持v=lm/s的恒定速率运行．一质量为m=4kg的行李无初速地放在A处，传送带对行李的滑动摩擦力使行李由静止开始做直线运动．已知行李在传送带上发生相对滑动时的加速度为1m/s2，AB间的距离L=2m，g=10m/s2．
（1）求行李由A运动到B的时间；
（2）如果提高传送带的运行速率，行李就能被较快地传送到B处．求行李从A处传送到B处的最短时间和传送带对应的最小运行速率．
如图，质量为M、长为L、高为h的矩形滑块置于水平地面上，滑块与地面间动摩擦因数为μ；滑块上表面光滑，其右端放置一个质量为m的小球．用水平外力击打滑块左端，使其在极短时间内获得向右的速度v0，经过一段时间后小球落地．求小球落地时距滑块左端的水平距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网