题目内容
如图甲所示,物体A、B的质量分别是4.0kg和8.0kg,用轻弹簧相连接放在光滑的水平面上,物体B左侧与竖直墙壁相接触,另有一物体C从t=0时刻起水平向左运动,在t=5.0s时与物体A相碰,并立即与A有相同的速度一起向左运动(但未粘连).物块C从向左至又和物体A脱离的速度-时间图象如图乙所示.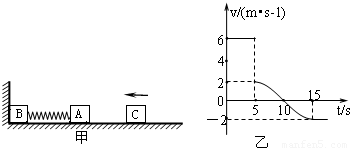
(1)求物块C的质量;
(2)在5s到15s的时间弹簧压缩过程中具有的最大弹性势能;
(3)在5s到15s的时间内墙壁对物体B的作用力的冲量的大小和方向;
(4)物体A与物块C脱离后至弹簧再次恢复原长时A、B的速度分别是多少?
【答案】分析:(1)由图象读出,物体C以6m/s的速度与A碰撞,碰撞后两者有相同的速度2m/s,根据动量守恒定律求出物块C的质量.
(2)物块C和A一起运动,压缩弹簧,当AC的速度减至零时,动能全部转化为弹簧的弹性势能,弹簧的弹性势能最大,根据机械能守恒定律求出弹簧的最大弹性势能.
(3)5s到5s的时间内,墙壁对B的作用力F等于轻弹簧的弹力,根据动量定理求解墙壁对物体B的作用力的冲量.
(4)物体A与物块C脱离后至弹簧再次恢复原长的过程中,AB系统的动量和机械能均守恒,由两大守恒定律求解再次恢复原长时A、B的速度.
解答:解:(1)由图象可得:物体C以速度v=6m/s与A相碰,碰撞后两者立即有相同的速度v=2m/s.A、C相互作用时间很短,水平方向动量守恒,有:
mCv=(mC+mA)v
解得:mC=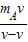 =2kg
=2kg
(2)物块C和A一起向左运动,压缩弹簧,当它们的动能完全转化为弹性势能,弹簧的弹性势能最大,最大的弹性势能为
EP= (mA+mC)v
(mA+mC)v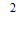 =12J
=12J
(3)在5s到15s内,墙壁对B的作用力F等于轻弹簧的弹力,轻弹簧的弹力使物体A和C的速度由2m/s减到0,再反弹到2m/s,则弹力的冲量等于F的冲量为:
I=(mA+mC)v-[-(mA+mC)v]=24N?s,方向向右.
(4)由图知,物体A与物块C脱离时速度大小为v=2m/s,方向向右.接着,A向右运动,弹簧伸长,B离开墙壁,AB组成的系统动量和机械能均守恒.
设弹簧再次恢复原长时A、B的速度分别vA和vB.取向右方向为正方向.
根据动量守恒和机械能守恒得:
mAv=mAv+mBvB
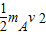 =
=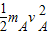 +
+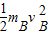
解得,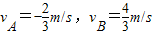
答:
(1)物块C的质量是2kg;
(2)弹簧压缩具有的最大弹性势能为12J.
(3)在5s到5s的时间内墙壁对物体B的作用力的冲量是24N?s,方向向右.(1)mC=2.0kg(2)EP=12J(3)I=24N?s,方向向右
(4)物体A与物块C脱离后至弹簧再次恢复原长时A、B的速度分别是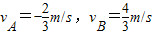 .
.
点评:点评:本题一要由速度图象读出物体的运动情况,明确碰撞前后A、C的速度,二要会根据动量守恒定律求解C的质量,由动量定理求解变力的冲量.
(2)物块C和A一起运动,压缩弹簧,当AC的速度减至零时,动能全部转化为弹簧的弹性势能,弹簧的弹性势能最大,根据机械能守恒定律求出弹簧的最大弹性势能.
(3)5s到5s的时间内,墙壁对B的作用力F等于轻弹簧的弹力,根据动量定理求解墙壁对物体B的作用力的冲量.
(4)物体A与物块C脱离后至弹簧再次恢复原长的过程中,AB系统的动量和机械能均守恒,由两大守恒定律求解再次恢复原长时A、B的速度.
解答:解:(1)由图象可得:物体C以速度v=6m/s与A相碰,碰撞后两者立即有相同的速度v=2m/s.A、C相互作用时间很短,水平方向动量守恒,有:
mCv=(mC+mA)v
解得:mC=
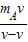 =2kg
=2kg(2)物块C和A一起向左运动,压缩弹簧,当它们的动能完全转化为弹性势能,弹簧的弹性势能最大,最大的弹性势能为
EP=
 (mA+mC)v
(mA+mC)v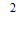 =12J
=12J(3)在5s到15s内,墙壁对B的作用力F等于轻弹簧的弹力,轻弹簧的弹力使物体A和C的速度由2m/s减到0,再反弹到2m/s,则弹力的冲量等于F的冲量为:
I=(mA+mC)v-[-(mA+mC)v]=24N?s,方向向右.
(4)由图知,物体A与物块C脱离时速度大小为v=2m/s,方向向右.接着,A向右运动,弹簧伸长,B离开墙壁,AB组成的系统动量和机械能均守恒.
设弹簧再次恢复原长时A、B的速度分别vA和vB.取向右方向为正方向.
根据动量守恒和机械能守恒得:
mAv=mAv+mBvB
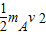 =
=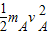 +
+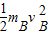
解得,
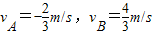
答:
(1)物块C的质量是2kg;
(2)弹簧压缩具有的最大弹性势能为12J.
(3)在5s到5s的时间内墙壁对物体B的作用力的冲量是24N?s,方向向右.(1)mC=2.0kg(2)EP=12J(3)I=24N?s,方向向右
(4)物体A与物块C脱离后至弹簧再次恢复原长时A、B的速度分别是
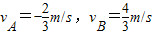 .
.点评:点评:本题一要由速度图象读出物体的运动情况,明确碰撞前后A、C的速度,二要会根据动量守恒定律求解C的质量,由动量定理求解变力的冲量.

练习册系列答案
相关题目
 如图甲所示,物体A正从斜面体B上沿斜面下滑,而斜面体在水平面上始终保持静止,物块沿斜面下滑运动的v-t图象如图乙所示,则下面说法中正确的是( )
如图甲所示,物体A正从斜面体B上沿斜面下滑,而斜面体在水平面上始终保持静止,物块沿斜面下滑运动的v-t图象如图乙所示,则下面说法中正确的是( )| A、物块A在沿斜面下滑的过程中受到两个力的作用 | B、物体A在沿斜面下滑的过程中受到三个力的作用 | C、地面对斜面体B有水平向左的摩擦力作用 | D、斜面体B相对于地面没有水平向左或向右的运动趋势 |
 如图甲所示,物体A正从斜面体B上沿斜面下滑,而斜面体在水平面上始终保持静止,物块沿斜面下滑运动的v-t图象如图乙所示,则下面说法中正确的是( )
如图甲所示,物体A正从斜面体B上沿斜面下滑,而斜面体在水平面上始终保持静止,物块沿斜面下滑运动的v-t图象如图乙所示,则下面说法中正确的是( )| A、物块A在沿斜面下滑的过程中受到两个力的作用 | B、物体A在沿斜面下滑的过程中受到三个力的作用 | C、地面对斜面体B有水平向左的摩擦力作用 | D、斜面体B相对于地面没有水平向左或向右的运动趋势 |
 如图甲所示,物体A重52N,物体B重24N,B用水平绳OC系住A与B,A与地面的动摩擦因数相同,若用20N的水平力F1拉A,恰能将A拉出,那么当绳OC与水平方向的夹角θ=45°时,如图乙,要用水平拉力F2将A拉出,则F2的大小至少是多大?
如图甲所示,物体A重52N,物体B重24N,B用水平绳OC系住A与B,A与地面的动摩擦因数相同,若用20N的水平力F1拉A,恰能将A拉出,那么当绳OC与水平方向的夹角θ=45°时,如图乙,要用水平拉力F2将A拉出,则F2的大小至少是多大?
