题目内容
如图所示，半径为R光滑半圆形轨道竖直放置，与水平轨道相接于最低点．两个质量均为m的小球A、B以不同的速度进入轨道内，A通过最高点C时，对管道上部压力为3mg，B恰好通过最高点C，求A、B两球落地点间的距离．
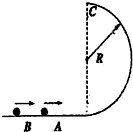
在圆轨道最高点，由牛顿第二定律得：
对A球，mg+N=m
，其中：N=3mg，解得：vA=2
，
B球恰好通过最高点，则在最高点，B球只受重力作用，
由牛顿第二定律得：mg=m
，解得：vB=
，
两球离开圆形轨道后都做平抛运动，
在竖直方向上：2R=
gt2，
在水平方向上：sA=vAt，sB=vBt，
两球落地点间的距离：△s=sA-sA，
解得：△s=2R；
答：A、B两球落地点间的距离为2R．
对A球，mg+N=m
| ||
| R |
| gR |
B球恰好通过最高点，则在最高点，B球只受重力作用，
由牛顿第二定律得：mg=m
| ||
| R |
| gR |
两球离开圆形轨道后都做平抛运动，
在竖直方向上：2R=
| 1 |
| 2 |
在水平方向上：sA=vAt，sB=vBt，
两球落地点间的距离：△s=sA-sA，
解得：△s=2R；
答：A、B两球落地点间的距离为2R．
练习册系列答案
阅读快车系列答案
相关题目
