题目内容
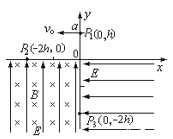
【题目】如图甲所示。在同一水平面上,两条足够长的平行金属导轨MNPQ间距为![]() ,右端接有电阻
,右端接有电阻![]() ,导轨EF连线左侧光滑且绝缘.右侧导轨粗糙,EFGH区域内有垂直导轨平面磁感应强度
,导轨EF连线左侧光滑且绝缘.右侧导轨粗糙,EFGH区域内有垂直导轨平面磁感应强度![]() 的矩形匀强磁场;一根轻质弹簧水平放置,左端固定在K点,右端与质量为
的矩形匀强磁场;一根轻质弹簧水平放置,左端固定在K点,右端与质量为![]() 的金属棒a接触但不栓接,且与导轨间的动摩擦因数
的金属棒a接触但不栓接,且与导轨间的动摩擦因数![]() ,弹簧自由伸长时a棒刚好在EF处,金属棒a垂直导轨放置,现使金属棒a在外力作用下缓慢地由EF向左压缩至AB处锁定,压缩量为
,弹簧自由伸长时a棒刚好在EF处,金属棒a垂直导轨放置,现使金属棒a在外力作用下缓慢地由EF向左压缩至AB处锁定,压缩量为![]() 。此时在EF处放上垂直于导轨质量
。此时在EF处放上垂直于导轨质量![]() 电阻
电阻![]() 的静止金属棒b。接着释放金属棒a,两金属棒在EF处碰撞,a弹回并压缩弹簧至CD处时速度刚好为零且被锁定,此时压缩量为
的静止金属棒b。接着释放金属棒a,两金属棒在EF处碰撞,a弹回并压缩弹簧至CD处时速度刚好为零且被锁定,此时压缩量为![]() ,b棒向右运动,经过
,b棒向右运动,经过![]() 从右边界GH离开磁场,金属棒b在磁场运动过程中流经电阻R的电量
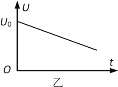
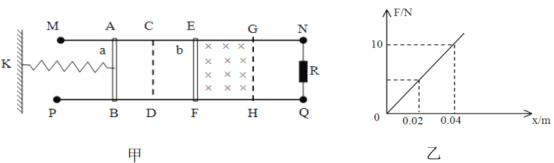
从右边界GH离开磁场,金属棒b在磁场运动过程中流经电阻R的电量![]() 。设棒的运动都垂直于导轨,棒的大小不计,已知弹簧的弹力与形变量的关系图像(如图乙)与x轴所围面积为弹簧具有的弹性势能。求:
。设棒的运动都垂直于导轨,棒的大小不计,已知弹簧的弹力与形变量的关系图像(如图乙)与x轴所围面积为弹簧具有的弹性势能。求:
(1)金属棒a碰撞金属棒b前瞬间的速度![]()
(2)金属棒b离开磁场时的速度![]()
(3)整个过程中电阻R上产生的热量![]()
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)如乙图所示,最初弹簧具有的弹性势能:
![]()
根据机械能守恒得:
![]()
可得 ![]()
(2)设![]() 棒反弹的速度为
棒反弹的速度为![]() ,
,![]() 棒碰后速度为
棒碰后速度为![]() ,金属棒
,金属棒![]() 离开磁场时的速度
离开磁场时的速度![]() 。
。
![]() 弹回至
弹回至![]() 处时弹簧具有的弹性势能为:
处时弹簧具有的弹性势能为:
![]()
根据机械能守恒得:
![]()
解得![]()
对于碰撞过程,取向右为正方向,由动量守恒定律得:
![]()
可得![]()
![]() 棒通过磁场的过程,根据动量定理得:
棒通过磁场的过程,根据动量定理得:
![]()
又:
![]()
![]()
可得![]()
(3)根据:
![]()
可得![]()
整个过程中回路产生的总热量:
![]()
电阻![]() 上产生的热量:
上产生的热量:
![]()
联立解得:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目