Question

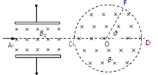
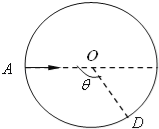
【题目】如图，一半径为R的圆表示一柱形区域的横截面（纸面），O为圆心．在柱形区域内加一方向垂直于纸面向外的匀强磁场，一质量为m、电荷量为+q的粒子沿图中直径从圆上的A点射入柱形区域，在圆上的D点离开该区域，已知图中θ=120°，现将磁场换为竖直向下的匀强电场，同一粒子以同样速度沿直径从A点射入柱形区域，也在D点离开该区域．若磁感应强度大小为B，不计重力，试求：

（1）电场强度E的大小；

（2）经磁场从A到D的时间与经电场从A到D的时间之比．

Answer 1

【答案】（1）电场强度E的大小是；

（2）经磁场从A到D的时间与经电场从A到D的时间之比是2π：9

【解析】

试题（1）加磁场时，粒子做匀速圆周运动，画出粒子在磁场中的运动轨迹图象，由几何关系可以得到轨道半径，进而由洛伦兹力提供向心力可得粒子初速度v0的大小；

粒子在匀强电场中粒子做类平抛运动，由平抛规律可得电场强度大小．

（2）粒子在磁场中运动时，根据轨迹的圆心角求解时间，由类平抛的规律得到电场运动的时间，即可解答．

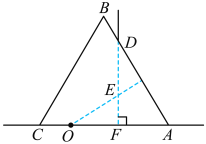
解：（1）加磁场时，粒子从A到D有：qBv0=m①

由几何关系有：r=Rtan=R ②

加电场时，粒子从A到D有：

R+Rcos60°=v0t ③

Rsin60°=④

由①～④得：E=⑤

（2）粒子在磁场中运动，由几何关系可知：圆心角α=60°

圆运动周期：T==⑦

经磁场的运动时间：t′=T=⑧

由①～④得粒子经电场的运动时间：t=⑨

即：=⑩

答：

（1）电场强度E的大小是；

（2）经磁场从A到D的时间与经电场从A到D的时间之比是2π：9．