题目内容
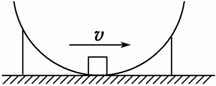
如图所示,半球形金属壳的半径为R,开口向上,竖直固定放置,质量为m的物块,沿着金属壳内壁滑下,滑到最低点时速度大小v,物块与球壳之间的动摩擦因数为μ,重力加速度为g,求:
(1)物块滑到最低点时向心加速度a向的大小和方向;
(2)物块在最低点受到的支持力N的大小;
(3)物块在最低点受到的摩擦力f的大小。
解:
(1)物块滑到最低点所需的向心力
![]() ① (2分)
① (2分)
根据牛顿第二定律
![]() ② (1分)
② (1分)
联立①、②两式解得向心加速度
![]() ③ (1分)
③ (1分)
向心加速度的方向竖直向上 (1分)
(2)物块在最低点由重力mg和支持力N的合力提供向心力
![]() ④ (2分)
④ (2分)
联立①、④两式解得支持力
![]() ⑤ (1分)
⑤ (1分)
(3)物块在最低点受到的摩擦力
![]() ⑥ (1分)
⑥ (1分)
联立⑤、⑥两式解得摩擦力
![]() ⑦ (1分)
⑦ (1分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
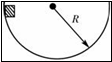 质量为m的物体沿着半径为r的半球形金属球壳滑到最低点时的速度大小为v,如图所示,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )
质量为m的物体沿着半径为r的半球形金属球壳滑到最低点时的速度大小为v,如图所示,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )A、受到的摩擦力为μm(g-
| ||
B、向心力为m(g+
| ||
C、对球壳的压力为
| ||
D、受到的摩擦力为μm(g+
|
 (2013?湖南模拟)如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )
(2013?湖南模拟)如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )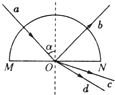 如图所示,一束复色光a从空气中以入射角α射向半球形玻璃砖球心O,在界面MN上同时发生反射和折射,分为b、c、d三束光,b为反射光,c、d为折射光,下列说法正确的是( )
如图所示,一束复色光a从空气中以入射角α射向半球形玻璃砖球心O,在界面MN上同时发生反射和折射,分为b、c、d三束光,b为反射光,c、d为折射光,下列说法正确的是( )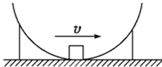 如图所示,半球形金属壳的半径为R,开口向上,竖直固定放置,质量为m的物块,沿着金属壳内壁滑下,滑到最低点时速度大小v,物块与球壳之间的动摩擦因数为μ,重力加速度为g,求:
如图所示,半球形金属壳的半径为R,开口向上,竖直固定放置,质量为m的物块,沿着金属壳内壁滑下,滑到最低点时速度大小v,物块与球壳之间的动摩擦因数为μ,重力加速度为g,求: