题目内容
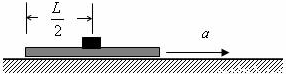
 一小圆盘静止在一长为L的薄滑板上,且位于滑板的中央,滑板放在水平地面上,如图所示.已知盘与滑板间的动摩擦因数为μ1,盘与地面间的动摩擦因数为μ2.现突然以恒定的加速度a(a>μ1g) 使滑板沿水平地面运动,加速度的方向是水平的且向右.若水平地面足够大,则小圆盘从开始运动到最后停止共走了多远?(以g 表示重力加速度)
一小圆盘静止在一长为L的薄滑板上,且位于滑板的中央,滑板放在水平地面上,如图所示.已知盘与滑板间的动摩擦因数为μ1,盘与地面间的动摩擦因数为μ2.现突然以恒定的加速度a(a>μ1g) 使滑板沿水平地面运动,加速度的方向是水平的且向右.若水平地面足够大,则小圆盘从开始运动到最后停止共走了多远?(以g 表示重力加速度)分析:根据牛顿第二定律求出圆盘子在滑板上运动时的加速度,根据匀变速直线运动的公式,抓住木板位移和圆盘位移之差为
求出圆盘的位移,圆盘在水平地面上做匀减速直线运动,根据牛顿第二定律求出加速度,根据匀变速直线运动速度位移公式求出匀减速运动位移,从而求出圆盘的总位移.
| L |
| 2 |
解答:解:圆盘在滑板上作匀加速运动,设圆盘刚离开滑板时,加速度为a1,速度为v1,位移为s1;滑板的位移为S0.
对圆盘有:
a1=μ1g
v1=a1t1
s1=
a1t12
对滑板有:
s0=
at12
又有:s0-s1=
联立各式解得:s1=
对圆盘离开滑板后作匀减速运动过程,设圆盘刚离开滑板到静止的位移为s2,加速度为a2.
对圆盘有:
a2=-μ2g
0-v12=2a2s2
联立解得:s2=
因此圆盘从开始运动到最后停止的位移为:s=s1+s2=
+
答:小圆盘从开始运动到最后停止共走了
+
.
对圆盘有:
a1=μ1g
v1=a1t1
s1=
| 1 |
| 2 |
对滑板有:
s0=
| 1 |
| 2 |
又有:s0-s1=
| L |
| 2 |
联立各式解得:s1=
| μ1gL |
| 2(a-μ1g) |
对圆盘离开滑板后作匀减速运动过程,设圆盘刚离开滑板到静止的位移为s2,加速度为a2.
对圆盘有:
a2=-μ2g
0-v12=2a2s2
联立解得:s2=
| μ12gL |
| 2μ2(a-μ1g) |
因此圆盘从开始运动到最后停止的位移为:s=s1+s2=
| μ1gL |
| 2(a-μ1g) |
| μ12gL |
| 2μ2(a-μ1g) |
答:小圆盘从开始运动到最后停止共走了
| μ1gL |
| 2(a-μ1g) |
| μ12gL |
| 2μ2(a-μ1g) |
点评:解决本题的关键理清圆盘在木板上和水平地面上的运动情况,灵活运用运动学公式求解.

练习册系列答案
相关题目

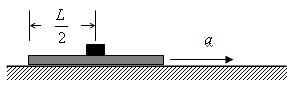
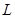 =2m的薄滑板(厚度不计)上,且位于滑板的中央,滑板放在水平地面上,如图所示.已知盘与滑板间的动摩擦因数为
=2m的薄滑板(厚度不计)上,且位于滑板的中央,滑板放在水平地面上,如图所示.已知盘与滑板间的动摩擦因数为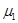 =0.2,盘与地面间的动摩擦因数为
=0.2,盘与地面间的动摩擦因数为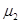 =0.5,现突然以恒定的加速度
=0.5,现突然以恒定的加速度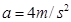 使滑板沿水平地面运动,加速度的方向水平向右.若水平地面足够大,则小圆盘从开始运动到最后停止共走了多远的距离?(重力加速度取
使滑板沿水平地面运动,加速度的方向水平向右.若水平地面足够大,则小圆盘从开始运动到最后停止共走了多远的距离?(重力加速度取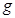 =10m/s2)
=10m/s2)