题目内容
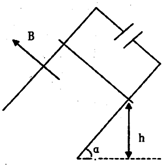
如图所示,两光滑导轨相距为L,倾斜放置,与水平地面夹角为θ,上端接一电容为C的电容器.导轨上有一质量为m长为L的导体棒平行地面放置,导体棒离地面的高度为h,磁感强度为B的匀强磁场与两导轨所决定的平面垂直,开始时电容器不带电.将导体棒由静止释放,整个电路电阻不计,则( )
| A.导体棒先做加速运动,后作匀速运动 | ||||
B.导体棒一直做匀加速直线运动,加速度为a=
| ||||
C.导体棒落地时瞬时速度v=
| ||||
| D.导体棒下落中减少的重力势能转化为动能,机械能守恒 |

A、设微小时间△t内电容器的带电量增加△q,I=
=
=
=CBLa ①,由牛顿第二定律得mgsinα-BIL=ma,解得:I=
②,由①②解得:a=
,故A错误,B正确;
C、导体棒做初速度为零的匀加速直线运动,由速度位移公式得:v2=2a
,解得:v=
,故C正确;
D、在导体棒运动过程中,重力做功把重力势能转化为动能,克服安培力做功,把重力势能转化为电场能,因此导体棒下落中减少的重力势能转化为动能和电场能,机械能不守恒,故D错误;
故选:BC.
| △q |
| △t |
| C△U |
| △t |
| CBL△v |
| △t |
| mgsinα-ma |
| BL |
| mgsinα |
| m+CB2L2 |
C、导体棒做初速度为零的匀加速直线运动,由速度位移公式得:v2=2a
| h |
| sinα |
|
D、在导体棒运动过程中,重力做功把重力势能转化为动能,克服安培力做功,把重力势能转化为电场能,因此导体棒下落中减少的重力势能转化为动能和电场能,机械能不守恒,故D错误;
故选:BC.

练习册系列答案
相关题目







