题目内容
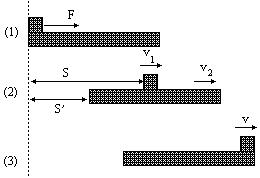
如图所示,长为L=1.0m、质量为M=1.0kg的木板,静止于光滑水平面上.在长木板的左端有一个质量为m=1.0kg的小木块(可视为质点).现用水平向右的恒力F=20N作用于小木块,使其由静止向右运动.作用一段距离后撤去水平力F,最终小木块恰好运动到长木板的右端.已知小木块与长木板间的动摩擦因数为μ=0.5,g=10m/s2.求:水平力F做功W为多少?
答案:
解析:
解析:
|
解:设水平力F作用时间为t1,撤去水平力F后再经过t2的时间,滑块滑到长木板的最右端,之后二者一起匀速运动,共同的速度为v.如图,在t1时间里小木块移动的距离为s,长木板移动距离为
F-μmg=ma 小木块的位移 s= 对整个系统由动量定理可得(亦可用牛顿定律及运动公式推出) Ft1=(M+m)v[或由三个式子合并而成,即 对系统由能量关系可得:Fs-μmgL= 联立以上各式并代数据有 s=0.75m 则拉力做功 W=Fs=20N×0.75m=15J |

练习册系列答案
相关题目
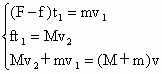 ]
]