Question

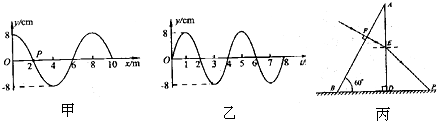
(13分)如图所示，质量为m＝10kg的小物体在F＝200N的水平推力作用下，从粗糙斜面的底端由静止开始沿足够长的斜面运动，斜面固定不动，小物体与斜面间的动摩擦因数μ＝0.25，斜面与水平地面间的夹角θ＝37°，力F作用t₁＝2s后撤去，小物体在斜面上继续上滑后，又返回至起点。(已知sin37°＝0.6，cos37°＝0.8，g取10m/s²)

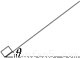
⑴小物体运动过程中相对起点的最大位移x_m的大小；

⑵小物体从开始经过多长时间t返回起点。

 

Answer 1

【答案】

 ⑴x_m＝16.25m；⑵t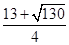＝s

【解析】

试题分析：⑴当物体上滑至最高点，速度为零时，相对起点的位移最大，设在t₁时间内物体运动的加速度为a₁，撤去力F瞬间时物体的速度为v，撤去力F后物体向上滑行的加速度为a₂，又经时间t₂物体的速度减为零，在有力F作用时，根据牛顿第二定律有：Fcosθ－mgsinθ－μ(Fsinθ＋mgcosθ)＝ma₁        ①

根据匀变速直线运动速度公式有：v＝a₁t₁       ②

撤去力F，物体继续上滑的过程中，根据牛顿第二定律有：－mgsinθ－μmgcosθ＝ma₂             ③

根据匀变速直线运动速度公式有：v＝－a₂t₂         ④

物体上滑的位移为：x_m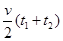＝          ⑤

由①②③④⑤式联立，并代入数据解得：t₂＝1.25s，x_m＝16.25m           ⑥

⑵物体下滑过程中，根据牛顿第二定律有：mgsinθ－μmgcosθ＝ma₃          ⑦

设物体下滑的时间为t₃，根据匀变速直线运动位移公式有：x_m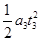＝          ⑧

物体从开始到返回起点的过程中所经历的时间为：t＝t₁＋t₂＋t₃           ⑨

由⑥⑦⑧⑨式联立，并代入数据解得：t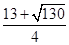＝s

考点：本题主要考查了匀变速直线运动规律、牛顿第二定律在多过程运动中的应用问题，属于中档题。