��Ŀ����
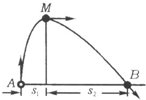 һС����A����ֱ�����׳����ڴ�������£��������Ĵ�С�㶨������ˮƽ���ң�С���˶��Ĺ켣��ͼ��ʾ��С����˶��ɿ�����ֱ�������ֱ�����˶���ˮƽ����ij���Ϊ����ȼ��ٶ�ֱ���˶��ĺ��˶�������С���˶��Ĺ켣��A��B���㴦��ͬһˮƽ���ϣ�M��Ϊ�켣����ߵ㣮С���׳��ij�����Ϊ5J��С������ߵ�M���Ķ���Ϊ2J���������������ƣ���
һС����A����ֱ�����׳����ڴ�������£��������Ĵ�С�㶨������ˮƽ���ң�С���˶��Ĺ켣��ͼ��ʾ��С����˶��ɿ�����ֱ�������ֱ�����˶���ˮƽ����ij���Ϊ����ȼ��ٶ�ֱ���˶��ĺ��˶�������С���˶��Ĺ켣��A��B���㴦��ͬһˮƽ���ϣ�M��Ϊ�켣����ߵ㣮С���׳��ij�����Ϊ5J��С������ߵ�M���Ķ���Ϊ2J���������������ƣ�����1��С��ˮƽλ��S1��S2֮�ȣ�
��2��С�������G�����ܷ���F�ı�ֵ��
��3��С����ص�B��ʱ�Ķ���EKB��
��4��С���A�㵽B����˶������У�С���ܵ���Сֵ��
��������1��С������ֱ����������ֱ�����˶������ݶԳ��Կ�֪��A����M��ʹ�M����B���ʱ��t��ȣ�С����ˮƽ������������Ϊ����ȼ����˶������˶�ѧ��ʽλ�ƹ�ʽ�����ñ��������S1��S2֮�ȣ�
��2��С���A�˶���M�����У���A����M���Ķ��ܣ��õ������ٶ��붯�ܵĹ�ϵʽ��������ֱ��ˮƽ��������ķ��˶������ٶȹ�ʽ��ţ�ٵڶ������������G�����ܷ���F�ı�ֵ��
��3���ֱ��о�A��M��A��Bˮƽ����ķ��˶������˶�ѧ��ʽ�ٶ�λ�ƹ�ϵʽ���С��B����ٶȣ����ɵõ�����EKB��
��4�������ٶȵĺϳɵõ�������ʱ��Ĺ�ϵʽ��������ѧ֪ʶ��ֵ���õ�С���ܵ���Сֵ��
��2��С���A�˶���M�����У���A����M���Ķ��ܣ��õ������ٶ��붯�ܵĹ�ϵʽ��������ֱ��ˮƽ��������ķ��˶������ٶȹ�ʽ��ţ�ٵڶ������������G�����ܷ���F�ı�ֵ��
��3���ֱ��о�A��M��A��Bˮƽ����ķ��˶������˶�ѧ��ʽ�ٶ�λ�ƹ�ϵʽ���С��B����ٶȣ����ɵõ�����EKB��
��4�������ٶȵĺϳɵõ�������ʱ��Ĺ�ϵʽ��������ѧ֪ʶ��ֵ���õ�С���ܵ���Сֵ��
����⣺��1��С������ֱ����������ֱ�����˶������ݶԳ��Ե�֪����A����M��ʹ�M����B���ʱ��t��ȣ�
С����ˮƽ������������Ϊ����ȼ���ֱ���˶�������ٶ�Ϊa����
S1=
at2
S2=
a(2t)2-
at2=
at2
����
=
��2�����⣬
m
=5J����vA=
����ֱ�����ϣ���vA=gt=
t������
=
t����
m
=2J����vM=
��ˮƽ�����ϣ��� vM=at=
t�����
=
t����
���Ԣ٣��ڵ�
=
��3��С����ˮƽ������
=2aS1��
=2a��S1+S2��=8aS1��
��
=4
С����ص�B��ʱ�Ķ���EKB=
m
=
m(
+
)=
m?4
+
m
=13J
��4����С���˶�ʱ��Ϊtʱ����ΪEk����
Ek=
m(v0-gt)2+
m(at)2
����Ϊ ��g2+a2��t2-2v0gt+
-
=0
����=0ʱ�м�ֵ��
��4
g2-4��g2+a2��(
-
)=0
��Ek=
Ek0
��
=
��a=
g
��Ekmin=
Ek0=
��5J=1.43J
��
��1��С��ˮƽλ��S1��S2֮��1��3��
��2��С�������G�����ܷ���F�ı�ֵ��
��
��
��3��С����ص�B��ʱ�Ķ���EKB��13J��
��4��С���A�㵽B����˶������У�С���ܵ���Сֵ��1.43J��
С����ˮƽ������������Ϊ����ȼ���ֱ���˶�������ٶ�Ϊa����
S1=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
����
| S1 |
| S2 |
| 1 |
| 3 |
��2�����⣬
| 1 |
| 2 |
| v | 2 A |
|
����ֱ�����ϣ���vA=gt=
| G |
| m |
|
| G |
| m |
| 1 |
| 2 |
| v | 2 M |
|
��ˮƽ�����ϣ��� vM=at=
| F |
| m |
|
| F |
| m |
���Ԣ٣��ڵ�
| G |
| F |
|
��3��С����ˮƽ������
| v | 2 M |
| v | 2 Bx |
��
| v | 2 Bx |
| v | 2 M |
С����ص�B��ʱ�Ķ���EKB=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 Bx |
| v | 2 By |
| 1 |
| 2 |
| v | 2 M |
| 1 |
| 2 |
| v | 2 A |
��4����С���˶�ʱ��Ϊtʱ����ΪEk����
Ek=
| 1 |
| 2 |
| 1 |
| 2 |
����Ϊ ��g2+a2��t2-2v0gt+
| v | 2 0 |
| 2Ek |
| m |
����=0ʱ�м�ֵ��
��4
| v | 2 0 |
| v | 2 0 |
| 2Ek |
| m |
��Ek=
| a2 |
| g2+a2 |
��
| G |
| F |
|
| ||
| 5 |
��Ekmin=
| 2 |
| 7 |
| 2 |
| 7 |
��
��1��С��ˮƽλ��S1��S2֮��1��3��
��2��С�������G�����ܷ���F�ı�ֵ��
| 5 |
| 2 |
��3��С����ص�B��ʱ�Ķ���EKB��13J��
��4��С���A�㵽B����˶������У�С���ܵ���Сֵ��1.43J��
���������������˶��ĺϳɺͷֽⷨ������ץס��ֱ�������˶��ĶԳ��Եõ�ʱ���ϵ�ǹؼ������ڵ�4�⣬Ҳ��������������ٶ���������ٶ��γɺϼ��ٶȣ����ٶȷ�����ϼ��ٶȷ���ֱʱ�ٶ���С��������С�������˶�ѧ��ʽ��ţ�ٵڶ����ɽ����⣮

��ϰ��ϵ�д�
�����Ŀ
 ��2004?���ݶ�ģ�����д�������£�һС����A����ֱ�����׳������˶��켣��ͼ��ʾ���켣��A��B������ͬһˮƽ���ϣ�M��Ϊ�켣����ߵ㣮�������Ĵ�С�㶨������ˮƽ���ң�С���׳�ʱ�Ķ���Ϊ4J����M��ʱ���Ķ���Ϊ2J������������������
��2004?���ݶ�ģ�����д�������£�һС����A����ֱ�����׳������˶��켣��ͼ��ʾ���켣��A��B������ͬһˮƽ���ϣ�M��Ϊ�켣����ߵ㣮�������Ĵ�С�㶨������ˮƽ���ң�С���׳�ʱ�Ķ���Ϊ4J����M��ʱ���Ķ���Ϊ2J������������������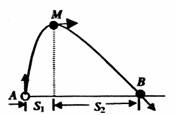 �ڴ�������£�һС����A����ֱ�����׳������˶��Ĺ켣��ͼ11��ʾ��С����˶��ɿ�����ֱ�������ֱ�����˶���ˮƽ����ij���Ϊ����ȼ���ֱ���˶��ĺ��˶�����С���˶��Ĺ켣��A��B������ͬһˮƽ���ϣ�M��Ϊ�켣����ߵ㡣�������Ĵ�С�㶨������ˮƽ���ң�С���׳�ʱ�Ķ���Ϊ4J����M��ʱ���Ķ���Ϊ2J��������������������
�ڴ�������£�һС����A����ֱ�����׳������˶��Ĺ켣��ͼ11��ʾ��С����˶��ɿ�����ֱ�������ֱ�����˶���ˮƽ����ij���Ϊ����ȼ���ֱ���˶��ĺ��˶�����С���˶��Ĺ켣��A��B������ͬһˮƽ���ϣ�M��Ϊ�켣����ߵ㡣�������Ĵ�С�㶨������ˮƽ���ң�С���׳�ʱ�Ķ���Ϊ4J����M��ʱ���Ķ���Ϊ2J��������������������