ЬтФПФкШн
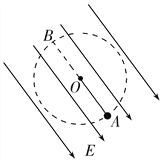
ЁОЬтФПЁПдкЙтЛЌОјдЕЫЎЦНУцЩЯЗХжУвЛжЪСПmЃН0.2 kgЁЂЕчКЩСПqЃНЃЋ5.0ЁС10Ѓ4 CЕФаЁЧђЃЌаЁЧђЯЕдкГЄLЃН0.5 m ЕФОјдЕЯИЯпЩЯЃЌЯИЯпЕФСэвЛЖЫЙЬЖЈдкOЕуЁЃећИізАжУжУгкдШЧПЕчГЁжаЃЌЕчГЁЗНЯђгыЫЎЦНУцЦНааЧвбиOAЗНЯђЃЌШчЭМ3ЫљЪО(ИЉЪгЭМ)ЁЃЯжИјаЁЧђвЛГѕЫйЖШЪЙЦфШЦOЕузідВжмдЫЖЏЃЌаЁЧђОЙ§AЕуЪБЯИЯпЕФеХСІFЃН140 NЃЌаЁЧђдкдЫЖЏЙ§ГЬжаЃЌзюДѓЖЏФмБШзюаЁЖЏФмДѓІЄEkЃН20 JЃЌаЁЧђПЩЪгЮЊжЪЕуЁЃ
(1)ЧѓЕчГЁЧПЖШЕФДѓаЁЃЛ
(2)ЧѓдЫЖЏЙ§ГЬжааЁЧђЕФзюаЁЖЏФмЃЛ
(3)ШєаЁЧђдЫЖЏЕНЖЏФмзюаЁЕФЮЛжУЪБЯИЯпБЛМєЖЯЃЌдђОЖрГЄЪБМфаЁЧђЖЏФмгыдкAЕуЪБЕФЖЏФмЯрЕШЃПДЫЪБаЁЧђОрAЕуЖрдЖЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() ЃЈ3ЃЉ
ЃЈ3ЃЉ![]()
![]()
ЁОНтЮіЁПЃЈ1ЃЉЩшAЕуЙигкOЕуЕФЖдГЦЕуЮЊBЃЌдђаЁЧђДгAдЫЖЏЕНBЕФЙ§ГЬжаЃЌЕчГЁСІзіИКЙІЃЌЖЏФмМѕаЁЃЌЫљвддкAЕуЖЏФмзюДѓЃЌдкBЕуЕФЖЏФмзюаЁЃЎ
аЁЧђдкЙтЛЌЫЎЦНУцЩЯдЫЖЏЕФзюДѓЖЏФмгызюаЁЖЏФмЕФВюжЕЮЊЁїEk=2qEL=20J
ДњШыЪ§ОнЕУЃКE=![]() N/C=4ЁС104N/C
N/C=4ЁС104N/C
ЃЈ2ЃЉдкAДІЃЌгЩХЃЖйЕкЖўЖЈТЩЃКF-qE=m![]() ЃЌ
ЃЌ
AДІаЁЧђЕФЖЏФмЮЊEkA=![]() mvA2=
mvA2=![]() ЃЈF-qEЃЉL=
ЃЈF-qEЃЉL=![]() ЁСЃЈ140-5.0ЁС10-4ЁС4ЁС104ЃЉЁС0.5=30ЃЈJЃЉ
ЁСЃЈ140-5.0ЁС10-4ЁС4ЁС104ЃЉЁС0.5=30ЃЈJЃЉ
аЁЧђЕФзюаЁЖЏФмЮЊ Ekmin=EkB=EkA-ЁїEk
ДњШыЪ§ОнЕУЃКEkB=30-20=10ЃЈJЃЉ
ЃЈ3ЃЉаЁЧђдкBДІЕФЖЏФмЮЊ EkB=![]() m vB2
m vB2
НтЕУЃК ![]()
ЕБаЁЧђЕФЖЏФмгыдкAЕуЪБЕФЖЏФмЯрЕШЪБЃЌгЩЖЏФмЖЈРэПЩжЊЃКy=2L
ЯпЖЯКѓЧђзіРрЦНХздЫЖЏЃК ![]()

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ


