题目内容
【题目】公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=4m,在距观景平台右侧边缘正前方d=4m处有垂直湖面足够大的宣传布幕.在P点左侧l=3m处湖底上的Q点安装有一单色光光源(可视为点光源).已知水对该单色光的折射率n=![]() ,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求:
,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求:

①该光源发出的光照射到布幕上的最高点距水面的高度h;
②该光源发出的光能射出水面的最远位置距观景平台右侧的最远距离s.
【答案】①3m②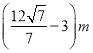
【解析】试题分析:射向观景台右侧边缘的光线折射后射到布幕上的位置最高,作出光路图,由数学知识求折射角的正弦值,即可由折射定律求出入射角的正弦,再由数学知识求解高度h.
Ⅱ、点光源S接近水面时,入射角为90°,光能照亮的距离最远,由折射定律求出折射角,即可由几何知识求解最远距离.
Ⅰ.光路如图所示:
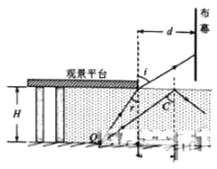
射向观景台右侧边缘的光线折射后射到布幕上的位置最高
由折射定律得: ![]()
而![]()
解得 sini=0.8
而 ![]()
解得 h=3m
Ⅱ、点光源S接近水面时,光在观景台右侧面与水面交接处掠射到水里时,被照亮的距离为最远距离,此时,入射角为90°,折射角为临界角C.
根据![]()
以及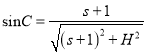
解得: 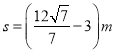

练习册系列答案
相关题目