题目内容
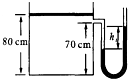（2013?商丘二模）一足够高的直立气缸上端开口，用一个厚度不计的活塞封闭了一段高为80cm的气柱，活塞的横截面积为0.01m2，活塞与气缸间的摩擦不计，气缸侧壁通过一个开口与U形管相连，开口离气缸底部的高度为70cm，开口管内及U形管内的气体体积忽略不计．已知如图所示状态时气体的温度为7 0C，U形管内水银面的高度差h1=5cm，大气压强p0=1.0×105 Pa保持不变，水银的密度| m |
| q |
| ||
| g |
①活塞的重力．
②现在活塞上添加沙粒，同时对气缸内的气体加热，始终保持活塞的高度不变，此过程缓慢进行，当气体的温度升高到37℃时，U形管内水银的高度差为多少？
分析：（1）封闭气体的压强可以以活塞为研究对象求出，也可以根据水银柱求出，即封闭气体的压强P=P0+
，又有P=P0+ρgh1，联立解得活塞的重力．
（2）活塞的高度不变，U形管内的气体体积忽略不计，则气缸内气体发生等容变化，根据查理定律求解U形管内水银的高度差．
| G活 |
| S |
（2）活塞的高度不变，U形管内的气体体积忽略不计，则气缸内气体发生等容变化，根据查理定律求解U形管内水银的高度差．
解答：解：①以活塞为研究对象，根据平衡条件：P0S+G活=PS，则P=P0+
，
又有P=P0+ρgh1，
即：p0+
=p0+ρgh1，
得：G活塞=ρgh1S=13.6×103×10×0.05×0.01N=68N．
②气缸内的气体近似做等容变化．
初状态：P=P0+ρgh1；温度为T1，
末状态：P=P0+ρgh2；温度为T2，
由查理定律：
=
可得h2=0.134 m．
答：（1）活塞的重力是68N．
（2）当气体的温度升高到37℃时，U形管内水银的高度差为0.134m．
| G活 |
| S |
又有P=P0+ρgh1，
即：p0+
| G活塞 |
| S |
得：G活塞=ρgh1S=13.6×103×10×0.05×0.01N=68N．
②气缸内的气体近似做等容变化．
初状态：P=P0+ρgh1；温度为T1，
末状态：P=P0+ρgh2；温度为T2，
由查理定律：
| p0+ρgh1 |
| T1 |
| p0+ρgh2 |
| T2 |
可得h2=0.134 m．
答：（1）活塞的重力是68N．
（2）当气体的温度升高到37℃时，U形管内水银的高度差为0.134m．
点评：本题是气体问题，确定气体状态作何种变化是关键，要充分挖掘隐含的条件进行分析．
练习册系列答案
名校课堂系列答案
相关题目
（2013?商丘二模）把电阻非线性变化的滑动变阻器接入图1的电路中，移动滑动变阻器触头改变接入电路中的长度x（x为图中a与触头之间的距离），定值电阻R1两端的电压与x间的关系如图2，a、b、c为滑动变阻器上等间距的三个点，当触头从a移到b和从b移到c的这两过程中，下列说法正确的是（ ）
（2013?商丘二模）如图所示，a、b、c、d是某匀强电场中的四个点，它们正好是一个矩形的四个顶点，ab=cd=L，ad=bc=2L，电场线与矩形所在平面平行．已知点a电势为20V，b点电势为24V，d点电势为12V．一个质子从b点以v0的速度射入此电场，入射方向与bc成450，一段时间后经过c点．不计质子的重力．下列判断正确的是（ ）
（2013?商丘二模）质量为m的物块在平行于斜面的力F作用下，从倾角为θ的固定斜面底端A由静止开始沿斜面上滑，经B点时速率为v，此时撤去F，物块滑回斜面底端时速率也为v，若A、B间距离为x，则（ ）
（2013?商丘二模）机械横波某时刻的波形图如图所示，波沿x轴正方向传播，质点p的坐标x=0.32m．从此时刻开始计时．