题目内容
9.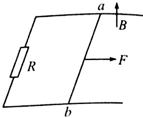 伽利略研究匀变速运动时曾提出这样的假设:匀加速直线运动的速度与位移成正比,我们称之为另类匀加速运动.类似也有另类匀减速运动,即物体速度随位移均匀减小.如图所示,两根足够长平行导轨固定在绝缘水平而上,导轨左端连接一个电阻,一根金属棒ab横跨在导轨上并与导轨垂直,不计导轨和金属棒的电阻. 整个装置置于竖直向上的匀强磁场中,金属棒开始时静止,在水平拉力作用一段时间后撤去,金属棒最终停下,不计一切摩擦.下列说法正确的是( )
伽利略研究匀变速运动时曾提出这样的假设:匀加速直线运动的速度与位移成正比,我们称之为另类匀加速运动.类似也有另类匀减速运动,即物体速度随位移均匀减小.如图所示,两根足够长平行导轨固定在绝缘水平而上,导轨左端连接一个电阻,一根金属棒ab横跨在导轨上并与导轨垂直,不计导轨和金属棒的电阻. 整个装置置于竖直向上的匀强磁场中,金属棒开始时静止,在水平拉力作用一段时间后撤去,金属棒最终停下,不计一切摩擦.下列说法正确的是( )| A. | 选取大小适当的水平恒力F,加速阶段可以是另类匀加速运动 | |
| B. | 撤去外力后,金属棒做减速运动一定恰好做另类匀减速运动 | |
| C. | 水平拉力做的功一定大于电阻产生的焦耳热 | |
| D. | 克服安培力做的功一定小于电阻产生的焦耳热 |
分析 A、根据牛顿第二定律,结合安培力综合表达式,及动能定理;
B、根据动能定理,结合安培力表达式;
CD、根据动能定理,结合克服安培力做的功即为电阻产生的焦耳热,即可求解.
解答 解:A、当选取大小适当的水平恒力F,根据牛顿第二定律,结合动能定理,
则有:(F-$\frac{{B}^{2}{L}^{2}v}{R}$)s=$\frac{1}{2}m{v}^{2}$,因此不能确定速度与位移的关系成正比,只有线性关系,故A错误;
B、撤去外力后,根据牛顿第二定律,结合动能定理,则有:-$\frac{{B}^{2}{L}^{2}v}{R}s$=0-$\frac{1}{2}m{v}^{2}$,解得:$v=\frac{2{B}^{2}{L}^{2}}{mR}s$,则有,物体速度随位移均匀减小,故B正确;
C、根据动能定理,水平拉力做的功与安培阻力做功之和,即为动能的增量,因棒的动能增加,因此水平拉力做的功一定大于电阻产生的焦耳热,故C正确;
D、由功能关系,可知,克服安培力做的功等于电阻产生的焦耳热,故D错误;
故选:BC.
点评 考查牛顿第二定律与动能定理的应用,掌握安培力综合表达式的内容,理解题目的已知条件,注意力做功的正负,及安培力做功与产生焦耳热的关系.

练习册系列答案
相关题目
19.质量为5m的机车以速度v运动,此时分别跟质量都为m的3节静止车厢挂接,挂接在一起时的速度为( )
| A. | $\frac{v}{3}$ | B. | $\frac{v}{5}$ | C. | $\frac{5v}{8}$ | D. | $\frac{v}{8}$ |
20.关于理想气体,下列说法正确的是( )
| A. | 气体的温度升高,所有分子的运动速率都增大 | |
| B. | 气体对容器的压强是由大量气体分子对启闭的频繁碰撞产生的 | |
| C. | 一定质量的气体,分子的平均动能越大,气体压强也越大 | |
| D. | 压缩理想气体是要用力,是因为分子间有斥力 |
4. 如图所示,一固定杆与水平方向夹角为θ=60°,将一质量为m的小环套在杆上,通过轻绳悬挂一个质量为m的小球由静止释放后,小环与小球保持相对静止以相同的速度.此时绳子与竖直方向夹角为β,杆对小环的摩擦力为f,则下列说法不正确的是( )
如图所示,一固定杆与水平方向夹角为θ=60°,将一质量为m的小环套在杆上,通过轻绳悬挂一个质量为m的小球由静止释放后,小环与小球保持相对静止以相同的速度.此时绳子与竖直方向夹角为β,杆对小环的摩擦力为f,则下列说法不正确的是( )
 如图所示,一固定杆与水平方向夹角为θ=60°,将一质量为m的小环套在杆上,通过轻绳悬挂一个质量为m的小球由静止释放后,小环与小球保持相对静止以相同的速度.此时绳子与竖直方向夹角为β,杆对小环的摩擦力为f,则下列说法不正确的是( )
如图所示,一固定杆与水平方向夹角为θ=60°,将一质量为m的小环套在杆上,通过轻绳悬挂一个质量为m的小球由静止释放后,小环与小球保持相对静止以相同的速度.此时绳子与竖直方向夹角为β,杆对小环的摩擦力为f,则下列说法不正确的是( )| A. | 若β=0°,则f=$\sqrt{3}$mg | B. | 若β=30°,则f=$\frac{\sqrt{3}}{3}$mg | ||
| C. | 若β=60°,则f=0 | D. | β有可能大于60° |
5.如图所示的两种电路中,电源相同,电源内阻不计,各电阻器阻值相等,各电流表的内阻相等且不可忽略不计.电流表A1、A2、A3和A4读出的电流值分别为I1、I2、I3和I4.下列关系式中正确的是( )
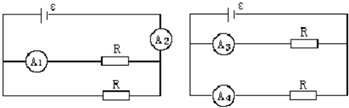

| A. | I1=I3 | B. | I1>I4 | C. | I2=2I1 | D. | I2<I3+I4 |
9.下列说法正确的是( )
| A. | 物体从外界吸收热量,其内能一定增加 | |
| B. | 热机的效率可以达到100% | |
| C. | 布朗运动是悬浮颗粒分子的无规则运动 | |
| D. | 叶面上的小露珠呈球形是由于液体表面张力的作用 |
10.关于电动势,下列说法错误的是( )
| A. | 电动势的单位是伏特 | |
| B. | 不同的电源的电动势一般是相等的 | |
| C. | 电动势的大小等于没有接入位外电路时电源两端的电压 | |
| D. | 电动势的大小由电源本身的性质来决定 |
 为了较准确地测量某细线能承受的最大拉力,小聪、小明分别进行了如下实验:
为了较准确地测量某细线能承受的最大拉力,小聪、小明分别进行了如下实验: