Question

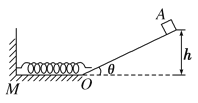
【题目】小物块A的质量为m=0.1kg，物块与坡道间的动摩擦因数为μ=0.125，水平面光滑；坡道顶端距水平面高度为h=0.48m，倾角为θ=37°；物块从坡道进入水平滑道时，在底端O点处无机械能损失，重力加速度为g=10m/s2。将轻弹簧的一端连接在水平滑道M处并固定在墙上，另一自由端恰位于坡道的底端O点，如图所示。物块A从坡顶由静止滑下，求：

(1)物块滑到O点时的速度大小。

(2)弹簧为最大压缩量时的弹性势能。

(3)物块A被弹回到坡道上升的最大高度。

Answer 1

【答案】（1）2m/s；（2）0.4J；（3）0.34m

【解析】

(1)由动能定理得mgh－μmghcotθ＝mv2，代入数据解得v＝=2m/s

(2)在水平滑道上，速度减为零时，弹簧有最大压缩量，由机械能守恒定律得：mv2＝Ep ，代入数据解得：Ep＝0.4J

(3)设物块A能够上升的最大高度为h1，物块被弹回过程中由动能定理得：－mgh1－μmgh1cotθ＝0－mv2 ，代入数据解得h1＝=0.34m