题目内容
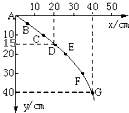 某同学在做“研究平抛物体运动”的实验中,忘记记下斜槽末端的位置O,A为物体运动一段时间后的位置,根据图所示图象,则物体平抛初速度为
某同学在做“研究平抛物体运动”的实验中,忘记记下斜槽末端的位置O,A为物体运动一段时间后的位置,根据图所示图象,则物体平抛初速度为2m/s
2m/s
、小球到D点时的速度2
m/s,与水平方向的夹角为45°
| 2 |
2
m/s,与水平方向的夹角为45°
.| 2 |
分析:抛运动竖直方向是自由落体运动,对于竖直方向根据△y=gT2求出时间单位T.对于水平方向由公式v0=
求出初速度,根据匀变速直线运动的时间中点的瞬时速度等于该过程中的平均速度,可以求出D点竖直方向的分速度,运用速度的合成,求解D的速度.
| x |
| T |
解答:解:设相邻两点间的时间间隔为T,竖直方向:△h=gT2,得到:
T=
=
=0.1s
水平方向匀速运动,因此有:x=2L=v0T
v0=
=2m/s
根据匀变速直线运动的时间中点的瞬时速度等于该过程中的平均速度,可得b点在竖直方向的速度为:
vDy=
=
=2m/s
b点速度的大小为:
v=
=2
m/s,
设与水平方向的夹角为θ,则tanθ=
=1,即与水平方向的夹角为45°.
故答案为:2m/s,2
m/s,与水平方向的夹角为45°.
T=
|
|
水平方向匀速运动,因此有:x=2L=v0T
v0=
| 0.2m |
| 0.1s |
根据匀变速直线运动的时间中点的瞬时速度等于该过程中的平均速度,可得b点在竖直方向的速度为:
vDy=
| hAG |
| 2T |
| 0.4m |
| 0.2s |
b点速度的大小为:
v=
|
| 2 |
设与水平方向的夹角为θ,则tanθ=
| vDy |
| v0 |
故答案为:2m/s,2
| 2 |
点评:解答这类问题的关键是抓住竖直方向自由落体运动的特点,由△y=△h=gT2求出时间,然后根据匀变速直线运动的规律和推论解题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 某同学在做研究平抛运动的实验中,忘了记下小球做平抛运动的起点位置.A为小球运动一段时间后的位置,将A记为坐标原点,根据图中所示数据,物体的平抛初速度大小为
某同学在做研究平抛运动的实验中,忘了记下小球做平抛运动的起点位置.A为小球运动一段时间后的位置,将A记为坐标原点,根据图中所示数据,物体的平抛初速度大小为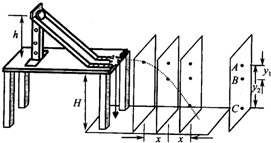 如图所示,是某同学在做“研究平抛物体运动”实验时的实验装置,在实验中用了一块平木板附上复写纸和白纸,竖直立于正对槽口前某处,使小球从斜槽上由静止滑下,小球撞在木板上留下痕迹A,将木板向后移距离x,再使小球从斜槽上同样高度由静止滑下,小球撞在木板上留下痕迹B,将木板再向后移距离x,小球再从斜槽上同样高度由静止滑下,再得到痕迹C,A、B间距离y1,A、C间距离y2.
如图所示,是某同学在做“研究平抛物体运动”实验时的实验装置,在实验中用了一块平木板附上复写纸和白纸,竖直立于正对槽口前某处,使小球从斜槽上由静止滑下,小球撞在木板上留下痕迹A,将木板向后移距离x,再使小球从斜槽上同样高度由静止滑下,小球撞在木板上留下痕迹B,将木板再向后移距离x,小球再从斜槽上同样高度由静止滑下,再得到痕迹C,A、B间距离y1,A、C间距离y2. 某同学在做“研究平抛物体的运动”的实验时得到了如图实所示的物体运动轨迹,a、b、c三点的位置在运动轨迹上已经标出,则(g取得m/s2)( )
某同学在做“研究平抛物体的运动”的实验时得到了如图实所示的物体运动轨迹,a、b、c三点的位置在运动轨迹上已经标出,则(g取得m/s2)( )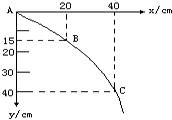 某同学在做“研究平抛物体运动”的实验中,忘了记录小球做平抛运动的起点位置S,A为物体运动一段时间后的位置,根据如图所示求出物体做平抛运动的初速度为
某同学在做“研究平抛物体运动”的实验中,忘了记录小球做平抛运动的起点位置S,A为物体运动一段时间后的位置,根据如图所示求出物体做平抛运动的初速度为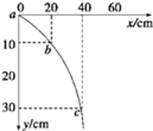 某同学在做“研究平抛物体的运动”的实验时得到了如图所示的物体轨迹,a、b、c三点的位置在轨迹上已经标出(a点不是抛出点),则小球的初速度v0=
某同学在做“研究平抛物体的运动”的实验时得到了如图所示的物体轨迹,a、b、c三点的位置在轨迹上已经标出(a点不是抛出点),则小球的初速度v0=