题目内容
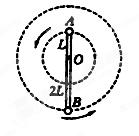
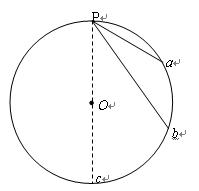
如图所示，Pa，Pb是竖直面内两根固定的光滑细杆，P，a，b，c位于同一圆周上，p点为圆周的最高点，c点为最低点，O为圆心．每根杆上都套着一个小滑环(图中未画出)．两个滑环都从P点无初速度释放，用t1，t2依次表示滑环到达a，b所用的时间，则：( )
| A．t1<t2 |
| B．t1＝t2 |
| C．若将P点从最高点向左侧移动一点点，则一定有t1>t2 |
| D．若将P点从最高点向左侧移动一点点，则一定有t1<t2 |
BC
试题分析：连接bc，设po与bc的夹角为
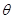，则有pb变为夹角为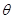得斜面，斜面长度为
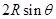，沿斜面下滑的加速度
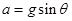，从P点无初速度释放则有
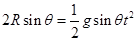得到
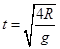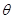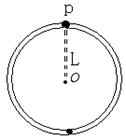
，可见运动时间与无关，可见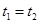
答案A错B对。若将P点从最高点向左侧移动一点点至
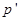，如下图所示，以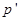为新的圆周的最高点，弦
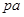的垂直平分线过圆心O点，与过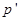的竖直线交点就是过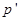和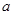
的新圆周的新圆心，根据前面的结论
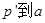时间
，同理弦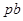
的垂直平分线过圆心O点，与过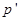的竖直线交点就是过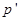和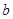
的新圆周的新圆心
时间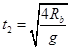
，根据几何关系
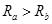所以
答案C对D错。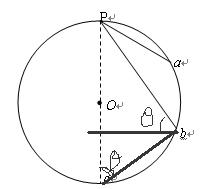
练习册系列答案
相关题目
