题目内容
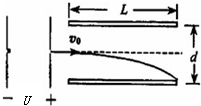
 一束电子流(一个电子电量为e=-1.6×10-19C)在电压U1=5000V的电场作用下由静止开始获得一定速度后,在距两极板等距离处垂直进入平行板间的匀强电场.如图所示,平行板的两板间距d=1.0cm,板长L=5.0cm.求:
一束电子流(一个电子电量为e=-1.6×10-19C)在电压U1=5000V的电场作用下由静止开始获得一定速度后,在距两极板等距离处垂直进入平行板间的匀强电场.如图所示,平行板的两板间距d=1.0cm,板长L=5.0cm.求:(1)要让电子能从平行板间飞出,两个极板上能加的最大电压U2是多大?
(2)在(1)的最大电压U2下,电子飞出电场的动能是多大?(结果可用eV表示)
分析:(1)根据动能定理求出电子加速获得的速度大小.电子进入偏转电场后做类平抛运动,恰好不飞出电场时,水平位移等于板长,竖直位移等于
,根据牛顿第二定律和运动学公式结合求出此时的电压U.
(2)对电子运动全过程运用动能定理,求解电子到达极板时的动能.
| d |
| 2 |
(2)对电子运动全过程运用动能定理,求解电子到达极板时的动能.
解答:解:(1)在加速电场中,根据动能定理得:qU1=
m
-0
电子进入偏转电场,因E⊥v0,故电子作类平抛运动,
水平方向:x=v0t
竖直方向:y=
at2=
由题,电子恰不飞出电场,
则有x=L,
y=
由此解得:U2=
=4×102V
(2)对电子运动全过程,运用动能定理,有 qU1+
=EK-0
则电子到达极板时动能EK=5.2×103eV
答:
(1)两板间至少要加4×102V 的电压U才能使电子恰不飞出电场.
(2)在上述电压下电子到达极板时的动能为5.2×103电子伏特.
| 1 |
| 2 |
| v | 2 0 |
电子进入偏转电场,因E⊥v0,故电子作类平抛运动,
水平方向:x=v0t
竖直方向:y=
| 1 |
| 2 |
| qU2t2 |
| 2md |
由题,电子恰不飞出电场,
则有x=L,
y=
| d |
| 2 |
由此解得:U2=
| 2U1d2 |
| L2 |
(2)对电子运动全过程,运用动能定理,有 qU1+
| qU2 |
| 2 |
则电子到达极板时动能EK=5.2×103eV
答:
(1)两板间至少要加4×102V 的电压U才能使电子恰不飞出电场.
(2)在上述电压下电子到达极板时的动能为5.2×103电子伏特.
点评:此题电子先经加速电场加速,后进入偏转电场偏转,根据动能定理求加速得到的速度,运用分解的方法研究类平抛运动,都是常规方法.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图所示,一束电子流以速率v从A 点射入,通过一个处于矩形空间的匀强磁场,进入磁场时的速度方向与磁感线垂直且沿 AB 边,若电子刚好从矩形磁场的 C 点离开磁场.(已知电子电量为e,质量为m,矩形磁场的边长AB=
如图所示,一束电子流以速率v从A 点射入,通过一个处于矩形空间的匀强磁场,进入磁场时的速度方向与磁感线垂直且沿 AB 边,若电子刚好从矩形磁场的 C 点离开磁场.(已知电子电量为e,质量为m,矩形磁场的边长AB=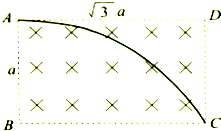 如图所示,一束电子流以速率v通过一个处于矩形空间的大小为B的匀强磁场,速度方向与磁感线垂直.且平行于矩形空间的其中一边,矩形空间边长为
如图所示,一束电子流以速率v通过一个处于矩形空间的大小为B的匀强磁场,速度方向与磁感线垂直.且平行于矩形空间的其中一边,矩形空间边长为