题目内容
如图所示，一束电子流以速率v从A 点射入，通过一个处于矩形空间的匀强磁场，进入磁场时的速度方向与磁感线垂直且沿 AB 边，若电子刚好从矩形磁场的 C 点离开磁场．（已知电子电量为e，质量为m，矩形磁场的边长AB=| 3 |
（ l ）该磁场的磁感应强度大小？（ 2 ）电子在磁场中的飞行时间？
分析：（1）找出圆心，画出轨迹，根据几何关系求出半径，再结合洛伦兹力提供向心力列式求解；
（2）根据时间等于弧长除以速度求解．
（2）根据时间等于弧长除以速度求解．
解答：解：（1）画出运动轨迹，如图所示
由几何关系：R=2a；
洛伦兹力提供向心力，有evB=m
解得：B=
（2）设圆心角为θ
sinθ=
θ=
故时间为：t=
=
=
=
答：（ l ）该磁场的磁感应强度大小为
；
（ 2 ）电子在磁场中的飞行时间
．
由几何关系：R=2a；
洛伦兹力提供向心力，有evB=m
| v2 |
| R |
解得：B=
| mv |
| 2ae |
（2）设圆心角为θ
sinθ=
| ||
| 2 |
| π |
| 3 |
故时间为：t=
| S |
| v |
R?
| ||
| v |
2a?
| ||
| v |
| 2πa |
| 3v |
答：（ l ）该磁场的磁感应强度大小为
| mv |
| 2ae |
（ 2 ）电子在磁场中的飞行时间
| 2πa |
| 3v |
点评：本题关键是找出圆心，画出轨迹，然后根据几何关系求出半径，最后根据洛伦兹力提供向心力列式求解．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，一束电子流沿管的轴线进入螺线管，忽略重力，电子在管内的运动应该是（ ）
如图所示，一束电子流在经U1=5000V的电压加速后，沿偏转极板的中线进入偏转电场中，已知偏转极板的长度L=5.0cm，间距d=1.0cm．试问：要使电子能从偏转极板顺利飞出，偏转电压U2不能超过多少？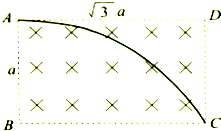
如图所示，一束电子流以速率v通过一个处于矩形空间的大小为B的匀强磁场，速度方向与磁感线垂直．且平行于矩形空间的其中一边，矩形空间边长为