Question

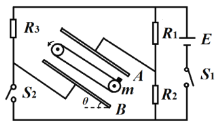
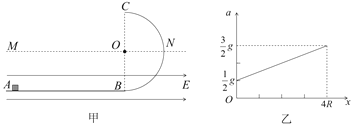
【题目】如图甲所示，粗糙水平轨道与半径为R的竖直光滑、绝缘的半圆轨道在B点平滑连接，过半圆轨道圆心O的水平界面MN的下方分布有水平向右的匀强电场E，质量为m的带正电小滑块从水平轨道上A点由静止释放，运动中由于摩擦起电滑块电量会增加，过B点后电量保持不变，小滑块在AB段加速度随位移变化图象如图乙。已知A、B间距离为4R，滑块与轨道间动摩擦因数为μ＝0.5，重力加速度为g，不计空气阻力，求：

(1)小滑块释放后运动至B点过程中电荷量的变化量；

(2)半圆轨道对小滑块的最大支持力大小；

(3)小滑块再次进入电场时，电场大小保持不变、方向变为向左，求小滑块再次到达水平轨道时距B的距离。

Answer 1

【答案】（1）（2）（3）6R。

【解析】

(1)由牛顿第二定律得，在点：

①

在点：

②

由①②联立解得：

③

(2)从到过程，由动能定理得：

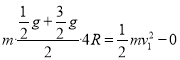④

将电场力与重力的合力等效为“重力”，与竖直方向的夹角设为，在“等效最低点”时滑块对轨道压力最大，则：

⑤

⑥

从到“等效最低点”过程，由动能定理得：

⑦

由牛顿第二定律得：

⑧

由②④⑤⑥⑦⑧式联立解得：

(3)从到过程，由动能定理得：

⑨

从点到再次进入电场的过程中做平抛运动：

水平方向：

⑩

竖直方向：

设速度方向与水平方向的夹角为，则有：

进入电场后，受向左的电场力与竖直向下的重力，则有：

由⑨⑩式联立可得：

则进入电场后合力与速度共线，做匀加速直线运动：

由⑨⑩式联立可得：

因此滑块再次到达水平轨道的位置在点左侧处。