题目内容
12.在20m高处以大小相等的初速度v0=20m/s,将三个质量均为0.1kg的小球a,b,c分别竖直上抛、平抛和竖直下落,从抛出到落地的全过程中,求重力对三个球做的功和平均功率.(不计空气阻力,g取10m/s2)分析 由W=mgh可以求出重力的功,应用匀变速直线运动的运动规律求出小球的运动时间,然后由功率公式求出平均功率.
解答 解:三个小球初末位置的高度差相同,重力做功相同,重力做的功都是:
W=mgh=0.1×10×20=20J,
a做竖直上抛运动,上升的高度:ha=$\frac{{v}_{0}^{2}}{2g}$=$\frac{2{0}^{2}}{2×10}$=20m,
小球上升时间:ta1=$\frac{{v}_{0}}{g}$=$\frac{20}{10}$=2s,
下降所用时间:ta2=$\sqrt{\frac{2(h+{h}_{a})}{g}}$=$\sqrt{\frac{2×(20+20)}{10}}$=2$\sqrt{2}$s,
a的运动时间:ta=ta1+ta2=(2+2$\sqrt{2}$)s,
重力的平均功率:Pa=$\frac{W}{{t}_{a}}$=$\frac{20}{2+2\sqrt{2}}$=$\frac{10}{1+\sqrt{2}}$W;
b做平抛运动,b的运动时间:tb=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×20}{10}}$=2s,
平均功率:Pb=$\frac{W}{{t}_{b}}$=$\frac{20}{2}$=10W;
c做竖直下抛运动,由物业公式得:h=v0tc+$\frac{1}{2}$gtc2,
即:20=20tc+$\frac{1}{2}$×10×tc2,解得:tc=(2$\sqrt{2}$-2)s,
重力的平均功率:Pc=$\frac{W}{{t}_{c}}$=$\frac{20}{2\sqrt{2}-2}$=$\frac{10}{\sqrt{2}-1}$W;
答:重力对三个球做的功都是20J,平均功率分半是:$\frac{10}{1+\sqrt{2}}$W、10W、$\frac{10}{\sqrt{2}-1}$W.
点评 本题考查了求功与功率问题,分析清楚小球的运动过程,知道小球的运动性质是正确解题的关键,应用功的计算公式、运动学公式与功率公式可以解题.

| X(m) | 0.200 | 0.400 | 0.600 | 0.700 | 0.800 | 0.900 | 0.950 |
| t(s) | 0.088 | 0.189 | 0.311 | 0.385 | 0.473 | 0.600 | 0.720 |
| $\frac{X}{t}$(m/s) | 2.27 | 2.12 | 1.93 | 1.82 | 1.69 | 1.50 | 1.32 |

请你根据题目所给数据完成下列问题(g=9.8m/s2,结果保留两位有效数字):
(1)根据表中所给的数据,在图2的坐标纸上画出$\frac{X}{t}$-t图线;
(2)根据所画出的$\frac{X}{t}$-t图线,得出滑块加速度的大小为a=3.0m/s2;
(3)滑块与水平长木板之间的动摩擦因数μ=0.31.
| A. | 甲 | B. | 乙 | ||
| C. | 丙 | D. | 条件不足,无法判断 |
 如图(a)所示,AB是某电场中的一条电场线.若带负电的粒子以某一初速度并且仅在电场力的作用下,沿AB由点A运动到点B,其速度图象如图(b)所示.下列关于A、B两点的电势ϕ和电场强度E和电势能EP大小的判断正确的是( )
如图(a)所示,AB是某电场中的一条电场线.若带负电的粒子以某一初速度并且仅在电场力的作用下,沿AB由点A运动到点B,其速度图象如图(b)所示.下列关于A、B两点的电势ϕ和电场强度E和电势能EP大小的判断正确的是( )| A. | EA<EB | |
| B. | 粒子从A点到B点过程,前半程电场力做功小于后半程的功 | |
| C. | φA>φB | |
| D. | EPA>EPB |
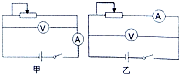 利用电流表和电压表测定一节干电池的电动势和内电阻.要求尽量减小实验误差.
利用电流表和电压表测定一节干电池的电动势和内电阻.要求尽量减小实验误差.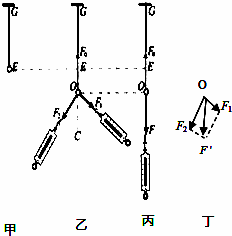 “探究求合力的方法”的实验如图所示,图甲轻质细绳套挂在橡皮条的下端,橡皮条的长度为GE;图乙中,用手通过弹簧测力计拉动细绳套,细绳套受到作用力F1、F2,橡皮条伸长,细绳套处于O点,这时它受到橡皮条对它向上的拉力F0;图丙是撤去F1、F2,改用一个力F拉住细绳套,仍使它处于O点,F1、F2、F的大小由弹簧测力计读出;图丁是在白纸上根据平行四边形定则画出的F′图示.
“探究求合力的方法”的实验如图所示,图甲轻质细绳套挂在橡皮条的下端,橡皮条的长度为GE;图乙中,用手通过弹簧测力计拉动细绳套,细绳套受到作用力F1、F2,橡皮条伸长,细绳套处于O点,这时它受到橡皮条对它向上的拉力F0;图丙是撤去F1、F2,改用一个力F拉住细绳套,仍使它处于O点,F1、F2、F的大小由弹簧测力计读出;图丁是在白纸上根据平行四边形定则画出的F′图示. 如图所示,水平放置的弹簧左端固定,小物块P(可视为质点)置于水平桌面上的A点,并与弹簧右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢地推至B点,此时弹簧的弹性势能为EP=21J.撤去推力后,P沿桌面滑上一个停在光滑水平地面上的长木板Q上,已知P、Q的质量分别为m=2kg、M=4kg,A、B间的距离Ll=4m,A距桌子边缘C的距离L2=2m,P与桌面及P与Q间的动摩擦因数都为μ=0.1,g取10m/s2,求:
如图所示,水平放置的弹簧左端固定,小物块P(可视为质点)置于水平桌面上的A点,并与弹簧右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢地推至B点,此时弹簧的弹性势能为EP=21J.撤去推力后,P沿桌面滑上一个停在光滑水平地面上的长木板Q上,已知P、Q的质量分别为m=2kg、M=4kg,A、B间的距离Ll=4m,A距桌子边缘C的距离L2=2m,P与桌面及P与Q间的动摩擦因数都为μ=0.1,g取10m/s2,求:



 如图所示,人重300N,物体重200N,地面粗糙,当人用100N的力向下拉绳子时,人和物体均处于静止状态,求:
如图所示,人重300N,物体重200N,地面粗糙,当人用100N的力向下拉绳子时,人和物体均处于静止状态,求: