题目内容
7.如图所示,光滑绝缘水平面上放置一单匝“L”形线框abcdef,线框质量为m,电阻为R,ab、bc、cd、de边长均为l.有一方向竖直向下的有界磁场,磁场的磁感应强度为B,磁场区宽度为2l,边界与bc边平行.线框在水平向右的拉力作用下以速度v匀速穿过磁场区域.求: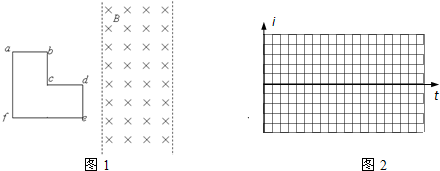
(1)在进入磁场过程中通过线框的电荷量q;
(2)线框穿过磁场区域过程中拉力做的功W;
(3)画出线框穿过磁场区域过程中,线框中电流随时间变化的i-t图线.(取逆时针方向为电流正方向).
分析 (1)根据法拉第电磁感应定律、欧姆定律和电量公式q=$\overline{I}$△t,求解电荷量q;
(2)线框匀速运动,拉力做功等于产生的焦耳热,分四段研究.
(3)由楞次定律判断出感应电流的方向,由法拉第电磁感应定律、欧姆定律求出感应电流的大小,再画出i-t图象.
解答 解:(1)在进入磁场过程中通过线框的电荷量为
q=$\overline{I}$△t=$\frac{\overline{E}}{R}△t$=$\frac{△Φ}{R}$=$\frac{B•3{l}^{2}}{R}$=$\frac{3B{l}^{2}}{R}$
(2)de进入至bc进入过程,感应电流 I1=$\frac{Blv}{R}$,沿逆时针方向
拉力做的功 W1=${I}_{1}^{2}Rt$=$\frac{{B}^{2}{l}^{3}v}{R}$
bc进入至af进入过程,感应电流 I2=$\frac{2Blv}{R}$,沿逆时针方向
拉力做的功 W2=${I}_{2}^{2}$Rt=$\frac{4{B}^{2}{l}^{3}v}{R}$
de离开至bc离开过程,感应电流 I3=$\frac{Blv}{R}$,沿顺时针方向
拉力做的功 W3=W1
bc离开至af离开过程,感应电流 I4=$\frac{2Blv}{R}$,沿顺时针方向
拉力做的功 W4=W2;
故拉力做的总功为 W=W1+W2+W3+W4=$\frac{10{B}^{2}{l}^{3}v}{R}$
(3)线框中电流随时间变化的i-t图线如图:
答:
(1)在进入磁场过程中通过线框的电荷量q是$\frac{3B{l}^{2}}{R}$;
(2)线框穿过磁场区域过程中拉力做的功W是$\frac{10{B}^{2}{l}^{3}v}{R}$;
(3)线框中电流随时间变化的i-t图线如图.
点评 解决本题的关键要熟练运用法拉第电磁感应定律、欧姆定律和电量公式q=$\overline{I}$△t,推导出电荷量表达式q=$\frac{△Φ}{R}$.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案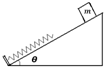 如图所示,一轻质弹簧下端固定在粗糙的斜面底端的挡板上,弹簧上端处于自由状态,斜面倾角为θ.一质量为m的物块(可视为质点)从离弹簧上端距离为L1处由静止释放,物块与斜面间动摩擦因数为?,物块在下滑过程中经A点(图中未画出)时速度最大为v,弹簧被压缩到最短时物体离释放点的距离为L2(重力加速度为g).从物块释放到弹簧压缩到最短的过程中( )
如图所示,一轻质弹簧下端固定在粗糙的斜面底端的挡板上,弹簧上端处于自由状态,斜面倾角为θ.一质量为m的物块(可视为质点)从离弹簧上端距离为L1处由静止释放,物块与斜面间动摩擦因数为?,物块在下滑过程中经A点(图中未画出)时速度最大为v,弹簧被压缩到最短时物体离释放点的距离为L2(重力加速度为g).从物块释放到弹簧压缩到最短的过程中( )| A. | 系统损失的机械能为?mg L2cosθ | |
| B. | 物体重力势能的减少量等于弹簧弹性势能的增加量与系统产生的内能之和 | |
| C. | 物块的速度最大时,弹簧的弹性势能为mgL1(sinθ-?cosθ)-$\frac{1}{2}$mv2 | |
| D. | 若物块能弹回,则上滑过程中经过A点时速度最大 |
 “快乐向前冲”节目中有这样一种项目,选手需要借助悬挂在高处的绳飞跃到鸿沟对面的平台上,如果已知选手的质量为m,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角为α,如图所示,不考虑空气阻力和绳的质量(选手可视为质点).下列说法正确的是( )
“快乐向前冲”节目中有这样一种项目,选手需要借助悬挂在高处的绳飞跃到鸿沟对面的平台上,如果已知选手的质量为m,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角为α,如图所示,不考虑空气阻力和绳的质量(选手可视为质点).下列说法正确的是( )| A. | 选手摆到最低点时所受绳子的拉力大于mg | |
| B. | 选手摆到最低点时受绳子的拉力大于选手对绳子的拉力 | |
| C. | 选手摆到最低点的运动过程中所受重力的功率一直增大 | |
| D. | 选手摆到最低点的运动过程为匀变速曲线运动 |
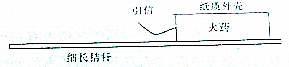 李华同学学习了《反冲运动•火箭》后,到商店买来喜庆用品“喜火”进行体验.“喜火”的结构如图所示.夜晚燃放时手持秸秆,点燃引信燃烧火药,当火焰从纸质外壳引信处向后喷出时“喜火”向前飞出,飞行距离大约为百米,并在空中划出一道红色曲线.测得“喜火”的总质量为M,如果把连续喷出的质量为m的气体简化为一次喷出,气体喷出的速度为v,则“喜火”飞出时的速度大小约为( )
李华同学学习了《反冲运动•火箭》后,到商店买来喜庆用品“喜火”进行体验.“喜火”的结构如图所示.夜晚燃放时手持秸秆,点燃引信燃烧火药,当火焰从纸质外壳引信处向后喷出时“喜火”向前飞出,飞行距离大约为百米,并在空中划出一道红色曲线.测得“喜火”的总质量为M,如果把连续喷出的质量为m的气体简化为一次喷出,气体喷出的速度为v,则“喜火”飞出时的速度大小约为( )| A. | $\frac{mv}{M}$ | |
| B. | $\frac{mv}{M-m}$ | |
| C. | $\frac{Mv}{M-m}$ | |
| D. | 因为不知道燃放时的高度,所以无法计算 |
| A. | 3v0-v | B. | 2v0-3v | C. | 3v0-2v | D. | 2v0+v |


 如图所示,一个$\frac{1}{4}$透明球体放置在水平面上,一束蓝光从A点沿水平方向射入球体后经B点射出,最后射到水平面上的C点.已知∠BOC=30°,∠BCO=30°,该球体对蓝光的折射率为$\sqrt{3}$;若换用一束红光同样从A点水平射向该球体,则它从球体射出后落到水平面上形成的光点与C点相比,位置偏右(填“偏左”、“偏右”或“不变”).
如图所示,一个$\frac{1}{4}$透明球体放置在水平面上,一束蓝光从A点沿水平方向射入球体后经B点射出,最后射到水平面上的C点.已知∠BOC=30°,∠BCO=30°,该球体对蓝光的折射率为$\sqrt{3}$;若换用一束红光同样从A点水平射向该球体,则它从球体射出后落到水平面上形成的光点与C点相比,位置偏右(填“偏左”、“偏右”或“不变”).