题目内容
4.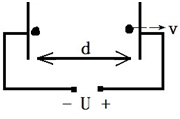 如图所示装置置于真空中,加速电场电压为U=1000V,两极板间距离为d;求电子由静止开始在装置中加速后离开电场时的速度v.
如图所示装置置于真空中,加速电场电压为U=1000V,两极板间距离为d;求电子由静止开始在装置中加速后离开电场时的速度v.
分析 电子在电场中,由于电场力做正功,电子的动能增大,由动能定理求速度v.
解答 解:电子的质量为m=9.1×10-31kg,电荷量 e=1.6×10-19C
根据动能定理得
eU=$\frac{1}{2}m{v}^{2}$
可得 v=$\sqrt{\frac{2eU}{m}}$=$\sqrt{\frac{2×1.6×1{0}^{-19}×1000}{9.1×1{0}^{-31}}}$≈1.88×107m/s
答:电子由静止开始在装置中加速后离开电场时的速度v是1.88×107m/s.
点评 对于电场加速过程,运用动能定理求速度是常用的方法,而且要知道v与d无关.

练习册系列答案
相关题目
16. 如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.在它从如图所示的位置转过90°的过程中,下列说法正确的是( )
如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.在它从如图所示的位置转过90°的过程中,下列说法正确的是( )
 如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.在它从如图所示的位置转过90°的过程中,下列说法正确的是( )
如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.在它从如图所示的位置转过90°的过程中,下列说法正确的是( )| A. | 通过电阻的电荷量为$\frac{NBSπ}{{2\sqrt{2}(R+r)}}$ | B. | 通过电阻的电荷量为$\frac{2NBS}{R+r}$ | ||
| C. | 外力所做的功为$\frac{{{N^2}{B^2}{S^2}ω}}{N(R+r)}$ | D. | 外力所做的功为$\frac{{π{N^2}{B^2}{S^2}ω}}{4(R+r)}$ |
14.某物体以30m/s的初速度竖直上抛,不计空气阻力,g取10m/s2,5s内物体的( )
| A. | 路程为65m | B. | 位移大小为25m,方向向上 | ||
| C. | 速度改变量为10m/s,方向向下 | D. | 平均速度为25m/s,方向向上 |

 如图所示,内壁光滑的木槽质量mA=0.1kg,内径为2m,置于水平桌面上,槽与桌面间的动摩擦因数为μ=0.3.槽内有两个可视为质点的小球B和C,它们的质量分别是mB=0.1kg、mC=0.2kg.现用两球将很短的轻弹簧压紧(球与弹簧不连接),且B球到木槽左端、C球到木槽右端的距离均为L=1m,这时弹簧的弹性势能为Ep=0.3J.同时释放B、C球,并假设小球与槽碰撞后不分离,碰撞时间极短,g=10m/s2,求:
如图所示,内壁光滑的木槽质量mA=0.1kg,内径为2m,置于水平桌面上,槽与桌面间的动摩擦因数为μ=0.3.槽内有两个可视为质点的小球B和C,它们的质量分别是mB=0.1kg、mC=0.2kg.现用两球将很短的轻弹簧压紧(球与弹簧不连接),且B球到木槽左端、C球到木槽右端的距离均为L=1m,这时弹簧的弹性势能为Ep=0.3J.同时释放B、C球,并假设小球与槽碰撞后不分离,碰撞时间极短,g=10m/s2,求: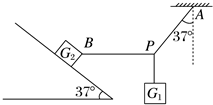 如图所示,重力G1=8N的砝码悬挂在绳PA和PB的结点上,PA偏离竖直方向37°角,PB水平且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,取g=10m/s2,已知cos37°=0.8,sin37°=0.6,试求:
如图所示,重力G1=8N的砝码悬挂在绳PA和PB的结点上,PA偏离竖直方向37°角,PB水平且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,取g=10m/s2,已知cos37°=0.8,sin37°=0.6,试求: