题目内容
4.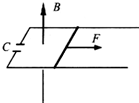 如图所示,光滑水平面上放置一平行金属导轨,其左端与平行板电容器C相连,一金属棒垂直金属导轨放置,整个装置处于垂直导轨平面向上的匀强磁场中.现对金属棒施加一水平向右的恒力F作用,使金属棒由静止开始运动,不计导轨及金属棒的电阻,则下面关于金属棒运动的速度v、加速度a、电容器两板间的电势差U、极板所带电量Q随时间t变化关系图象中,正确的是( )
如图所示,光滑水平面上放置一平行金属导轨,其左端与平行板电容器C相连,一金属棒垂直金属导轨放置,整个装置处于垂直导轨平面向上的匀强磁场中.现对金属棒施加一水平向右的恒力F作用,使金属棒由静止开始运动,不计导轨及金属棒的电阻,则下面关于金属棒运动的速度v、加速度a、电容器两板间的电势差U、极板所带电量Q随时间t变化关系图象中,正确的是( )| A. | 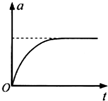 | B. | 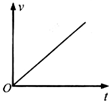 | C. | 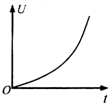 | D. | 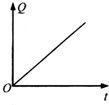 |
分析 解答本题先分析金属棒的运动情况:
金属棒在向右运动的过程中,随着速度增大,安培力增大,由牛顿第二定律分析加速度的变化,推导出各物理量随时间的变化情况进行解答.
解答 解:A、根据动量定理可得Ft-BILt=m△v,所以a=$\frac{F-BIL}{m}$;
根据电流的定义式:I=$\frac{△q}{△t}=\frac{CU}{△t}$
根据法拉第电磁感应定律:U=BL△v
整理以上式子得:I=$\frac{CBL△v}{△t}$=CBLa
所以有:a=$\frac{F}{m+{B}^{2}{L}^{2}C}$为一定值,导体棒做匀加速直线运动,A错误;
B、根据v=at可知B正确;
C、根据法拉第电磁感应定律:U=BL△v=BLat,C错误;
D、极板所带电量Q随时间t变化关系为:Q=CU=CBLat,D正确;
故选:BD.
点评 本题是导体在导轨上滑动的类型,类似于汽车的起动问题,抓住安培力大小与速度大小成正比,进行动态分析.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.关于摩擦力做功的下列说法中正确的是( )
| A. | 滑动摩擦力阻碍物体的相对运动,一定做负功 | |
| B. | 静摩擦力有阻碍物体的相对运动趋势的作用,一定不做功 | |
| C. | 静摩擦力和滑动摩擦力都可能做正功 | |
| D. | 作用力做正功,反作用力一定做负功 |
10.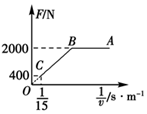 质量为8×102kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象(图中AB、BO均为直线),假设电动车行驶中所受的阻力恒定,则( )
质量为8×102kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象(图中AB、BO均为直线),假设电动车行驶中所受的阻力恒定,则( )
 质量为8×102kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象(图中AB、BO均为直线),假设电动车行驶中所受的阻力恒定,则( )
质量为8×102kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象(图中AB、BO均为直线),假设电动车行驶中所受的阻力恒定,则( )| A. | 在全过程中,电动车在B点时速度最大 | |
| B. | AB过程电动车做匀变速运动 | |
| C. | BC过程电动车的牵引力功率不变 | |
| D. | BC过程电动车做减速运动 |
7. 如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出从y轴上沿x轴正向抛出的三个小球a,b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则( )
如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出从y轴上沿x轴正向抛出的三个小球a,b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则( )
 如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出从y轴上沿x轴正向抛出的三个小球a,b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则( )
如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出从y轴上沿x轴正向抛出的三个小球a,b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则( )| A. | a在空中运动的时间比b的长 | B. | b和c在空中运动的时间相同 | ||
| C. | a的初速度比b的小 | D. | b的初速度比c的大 |
14. 如图所示,A、B是真空中的两个等量异种点电荷,M、N、O是AB连线的垂线上的点,且AO>OB,一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,M、N为轨迹和垂线的交点,设M、N两点的场强大小分别为EM、EN,电势分别为φM、φN,下列说法中正确的是( )
如图所示,A、B是真空中的两个等量异种点电荷,M、N、O是AB连线的垂线上的点,且AO>OB,一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,M、N为轨迹和垂线的交点,设M、N两点的场强大小分别为EM、EN,电势分别为φM、φN,下列说法中正确的是( )
 如图所示,A、B是真空中的两个等量异种点电荷,M、N、O是AB连线的垂线上的点,且AO>OB,一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,M、N为轨迹和垂线的交点,设M、N两点的场强大小分别为EM、EN,电势分别为φM、φN,下列说法中正确的是( )
如图所示,A、B是真空中的两个等量异种点电荷,M、N、O是AB连线的垂线上的点,且AO>OB,一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,M、N为轨迹和垂线的交点,设M、N两点的场强大小分别为EM、EN,电势分别为φM、φN,下列说法中正确的是( )| A. | EM小于EN | |
| B. | 点电荷A一定带正电 | |
| C. | φM大于φN | |
| D. | 此试探电荷在M处的电势能小于N处的电势能 |
9. A和L是日光灯的灯管和镇流器,如果按图所示的电路连接,下列关于日光灯发光情况的叙述中,正确的是( )
A和L是日光灯的灯管和镇流器,如果按图所示的电路连接,下列关于日光灯发光情况的叙述中,正确的是( )
 A和L是日光灯的灯管和镇流器,如果按图所示的电路连接,下列关于日光灯发光情况的叙述中,正确的是( )
A和L是日光灯的灯管和镇流器,如果按图所示的电路连接,下列关于日光灯发光情况的叙述中,正确的是( )| A. | 只把S1接通,S2、S3不接通,日光灯就能正常发光 | |
| B. | 把S1和S2接通后,S3不接通,日光灯就能正常发光 | |
| C. | 当日光灯正常发光后,再接通S3,日光灯仍能正常发光 | |
| D. | S3不接通,接通S1和S2后再断开S2,日光灯就能正常发光 |
16.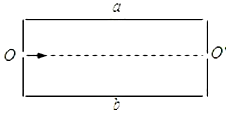 图中为一“滤速器”装置示意图,a、b 为水平放置的平行金属板,一束具有 各种不同速率的电子沿水平方向经小孔 O 进入 a、b 两板之间.为了选取具有某 种特定速率的电子,可在 a、b 间加上电压,并沿垂直于纸面的方向加一匀强磁 场,使所选 电子仍能够沿水平直线 OO'运动,由 O'射出.不计重力作用.可能 达到上述目的办法是( )
图中为一“滤速器”装置示意图,a、b 为水平放置的平行金属板,一束具有 各种不同速率的电子沿水平方向经小孔 O 进入 a、b 两板之间.为了选取具有某 种特定速率的电子,可在 a、b 间加上电压,并沿垂直于纸面的方向加一匀强磁 场,使所选 电子仍能够沿水平直线 OO'运动,由 O'射出.不计重力作用.可能 达到上述目的办法是( )
 图中为一“滤速器”装置示意图,a、b 为水平放置的平行金属板,一束具有 各种不同速率的电子沿水平方向经小孔 O 进入 a、b 两板之间.为了选取具有某 种特定速率的电子,可在 a、b 间加上电压,并沿垂直于纸面的方向加一匀强磁 场,使所选 电子仍能够沿水平直线 OO'运动,由 O'射出.不计重力作用.可能 达到上述目的办法是( )
图中为一“滤速器”装置示意图,a、b 为水平放置的平行金属板,一束具有 各种不同速率的电子沿水平方向经小孔 O 进入 a、b 两板之间.为了选取具有某 种特定速率的电子,可在 a、b 间加上电压,并沿垂直于纸面的方向加一匀强磁 场,使所选 电子仍能够沿水平直线 OO'运动,由 O'射出.不计重力作用.可能 达到上述目的办法是( )| A. | 使 a 板电势高于 b 板,磁场方向垂直纸面向里 | |
| B. | 使 a 板电势低于 b 板,磁场方向垂直纸面向里 | |
| C. | 使 a 板电势高于 b 板,磁场方向垂直纸面向外 | |
| D. | 使 a 板电势低于 b 板,磁场方向垂直纸面向外 |
13.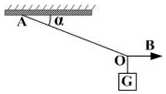 如图所示,一定质量的物块用两根轻绳悬在空中,其中绳OA固定不变,绳OB在竖直平面内由水平方向向上转动,则在绳OB由水平转至竖直的过程中,绳OA的张力和绳OB的张力的大小将( )
如图所示,一定质量的物块用两根轻绳悬在空中,其中绳OA固定不变,绳OB在竖直平面内由水平方向向上转动,则在绳OB由水平转至竖直的过程中,绳OA的张力和绳OB的张力的大小将( )
 如图所示,一定质量的物块用两根轻绳悬在空中,其中绳OA固定不变,绳OB在竖直平面内由水平方向向上转动,则在绳OB由水平转至竖直的过程中,绳OA的张力和绳OB的张力的大小将( )
如图所示,一定质量的物块用两根轻绳悬在空中,其中绳OA固定不变,绳OB在竖直平面内由水平方向向上转动,则在绳OB由水平转至竖直的过程中,绳OA的张力和绳OB的张力的大小将( )| A. | OA绳的张力一直变大 | B. | OA绳的张力一直变小 | ||
| C. | OB绳的张力先变大后变小 | D. | OB绳的张力先变小后变大 |
14.一个质点在做曲线运动,下列说法正确的是( )
| A. | 速度一定在不断改变,加速度也一定不断改变 | |
| B. | 质点不可能在做匀变速运动 | |
| C. | 若该质点做圆周运动,其加速度是变化的,方向一定指向圆心 | |
| D. | 质点速度方向在时刻变化,一定在做变速运动 |