题目内容
14.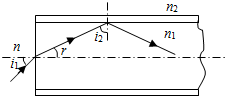 设光导纤维由折射率为n1的玻璃芯和折射率为n2(n1>n2)的同轴外套构成,如图所示,横截端面外的媒质折射率为n,试求能使光线在纤维内发生全反射的入射光束的最大孔径角i1,即最大入射角i1.已知介质2的折射率与介质1的折射率之比称为介质2对介质1的相对折射率,用n12表示.(结果可用反三角函数表示)
设光导纤维由折射率为n1的玻璃芯和折射率为n2(n1>n2)的同轴外套构成,如图所示,横截端面外的媒质折射率为n,试求能使光线在纤维内发生全反射的入射光束的最大孔径角i1,即最大入射角i1.已知介质2的折射率与介质1的折射率之比称为介质2对介质1的相对折射率,用n12表示.(结果可用反三角函数表示)
分析 根据题意,当i2恰好等于临界角时,则有最大入射角i1.再由sinC=$\frac{1}{n}$,结合折射定律,即可求解.
解答 解:根据光的全反射条件,当i2=C,恰好发生光的全反射,那么即有最大入射角i1.
若i2继续增大,仍有全反射,但入射角i1不是最大的,
因此sinC=$\frac{{n}_{2}}{{n}_{1}}$=sini2,
而i2+r=$\frac{π}{2}$;
则cosr=$\frac{{n}_{2}}{{n}_{1}}$;
那么sinr=$\sqrt{1-(\frac{{n}_{2}}{{n}_{1}})^{2}}$
再由光的折射定律,则有:$\frac{sin{i}_{1}}{sinr}$=$\frac{{n}_{1}}{{n}_{\;}}$;
则有:sini1=$\frac{{n}_{1}}{n}$$\sqrt{1-(\frac{{n}_{2}}{{n}_{1}})^{2}}$=$\frac{\sqrt{{n}_{1}^{2}-{n}_{2}^{2}}}{n}$
解得:最大入射角i1=arcsin$\frac{\sqrt{{n}_{1}^{2}-{n}_{2}^{2}}}{n}$.
答:能使光线在纤维内发生全反射的入射光束的最大入射角为arcsin$\frac{\sqrt{{n}_{1}^{2}-{n}_{2}^{2}}}{n}$.
点评 考查光的折射定律,掌握全反射中临界角与折射率的关系,理解相对折射率的含义,注意反三角函数,及确定正确的几何关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.质量为m1和m2的两个物体分别受到不同恒定外力F1和F2的作用,设它们从静止开始运动,通过相同的位移,两个物体的动量的增量相同,则F1和F2满足的关系为( )
| A. | F1:F2=m1:m2 | B. | F1:F2=m2:m1 | C. | F1:F2=$\sqrt{{m}_{1}}$:$\sqrt{{m}_{2}}$ | D. | F1:F2=$\sqrt{{m}_{2}:{m}_{1}}$ |
19.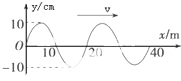 在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚好传播到x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是( )
在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚好传播到x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是( )
 在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚好传播到x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是( )
在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚好传播到x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是( )| A. | 波源开始振动时方向沿y轴正方向 | |
| B. | 从t=0开始经0.15s,x=40m的质点运动的路程为0.6m | |
| C. | 接收器在t=2s时才能接收到此波 | |
| D. | 当波刚刚传到接收器时,x=20m的质点速度刚好为0 |
12.设想地磁场是由地球内部的环形电流形成的,那么这一环形电流的方向应该是( )
| A. |  由东向西 | B. |  由西向东 | C. |  由南向北 | D. | 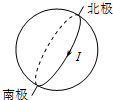 由北向南 |
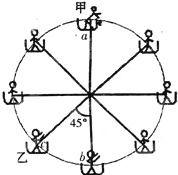 游乐园的小型“摩天轮”上对称站着质量均为m的8位同学,如图所示,“摩天轮”在竖直平面内逆时针匀速转动,若某时刻转到顶点a上的甲同学让一小重物做自由落体运动,并立即通知下面的同学接住,结果重物掉落时正处在c处(如图)的乙同学恰好在第一次到达最低点b处接到,己知“摩天轮”半径为R,重力加速度为g,(不计人和吊篮的大小及重物的质量),问:
游乐园的小型“摩天轮”上对称站着质量均为m的8位同学,如图所示,“摩天轮”在竖直平面内逆时针匀速转动,若某时刻转到顶点a上的甲同学让一小重物做自由落体运动,并立即通知下面的同学接住,结果重物掉落时正处在c处(如图)的乙同学恰好在第一次到达最低点b处接到,己知“摩天轮”半径为R,重力加速度为g,(不计人和吊篮的大小及重物的质量),问: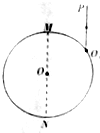 如图所示的圆表示一圆柱形玻璃砖的截面,O为其圆心,MN为直径.一束平行于MN的光线沿PO1方向从O1点射入玻璃砖,在玻璃砖内传到N点,已知PO1与MN之间的距离为$\frac{\sqrt{3}}{2}$R(R为玻璃砖的半径),真空中的光速为c,求:
如图所示的圆表示一圆柱形玻璃砖的截面,O为其圆心,MN为直径.一束平行于MN的光线沿PO1方向从O1点射入玻璃砖,在玻璃砖内传到N点,已知PO1与MN之间的距离为$\frac{\sqrt{3}}{2}$R(R为玻璃砖的半径),真空中的光速为c,求: