题目内容
假设一个沿着一定方向运动的光子和一个静止的自由电子发生碰撞后，电子向某一方向运动，光子将偏离原来的运动方向，这种现象称为光子的散射，散射后的光子跟原来相比
| A．光子将从电子处获得能量，因而频率增大 |
| B．散射后的光子运动方向将与电子运动方向在一条直线上 |
| C．由于电子受到碰撞，散射光子的频率低于入射光子的频率 |
| D．散射光子虽改变原来的运动方向，但频率不变. |
C
解析试题分析：由碰撞知识可得：光子与电子碰撞，一部分能量转移给电子，所以光子能量减小，根据
可得
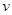减小，即光子频率减小．所以散射后光子的频率小于入射光子的频率．故AD错误，C正确；光子与电子碰撞后偏离原来的运动方向，根据动量守恒知，散射后光子的运动方向与电子的运动方向不在同一条直线上．故B错误．
考点：本题关键抓住动量守恒和能量守恒，以及波速、波长、频率的关系进行分析求解．
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案在光滑的水平桌面上有等大的质量分别为M="0.6" kg，m="0.2" kg的两个小球，中间夹着一个被压缩的具有Ep="10.8" J弹性势能的轻弹簧（弹簧与两球不相连），原来处于静止状态.现突然释放弹簧，球m脱离弹簧后滑向与水平面相切、半径为R="0.425" m的竖直放置的光滑半圆形轨道，如图所示.g取10 m/s2.则下列说法正确的是：
| A．球m从轨道底端A运动到顶端B的过程中所受合外力冲量大小为3.4 N·s |
| B．M离开轻弹簧时获得的速度为9m/s |
| C．若半圆轨道半径可调，则球m从B点飞出后落在水平桌面上的水平距离随轨道半径的增大而减小 |
| D．弹簧弹开过程，弹力对m的冲量大小为1.8 N·s |
如图所示，小车与木箱紧挨着静放在光滑的水平冰面上，现有一男孩站在小车上用力向右迅速推出木箱，关于上述过程，下列说法中正确的是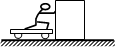 
| A．男孩和木箱组成的系统动量守恒 |
| B．小车与木箱组成的系统动量守恒 |
| C．男孩、小车与木箱三者组成的系统动量守恒 |
| D．木箱的动量增量与男孩、小车的总动量增量相同 |
一颗手榴弹以v0=10m/s的水平速度在空中飞行。设它爆炸后炸裂为两块，小块质量为0.2 kg，沿原方向以250 m/s的速度飞去，那么，质量为0.4 kg的大块在爆炸后速度大小和方向是
| A．125 m/s，与v0反向 |
| B．110 m/s，与v0反向 |
| C．240 m/s，与v0反向 |
| D．以上答案均不正确 |
K－介子衰变的方程为：K－→
，其中
介子和
介子带负电，电量为元电荷，
介子不带电，一个介子沿垂直于磁场的方向射入匀强磁场中，其轨迹为圆弧AP，衰变后产生的介子的轨迹为圆弧PB，两轨迹在P点相切如图所示，它们的半径
之比为2：1.介子的轨迹未画出.由此可知的动量大小与的动量大小之比为（ ） 
| A．1：1 | B．1：2 | C．1：3 | D．1：6 |
右端带有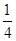
光滑圆弧轨道质量为M的小车静置于光滑水平面上，如图所示．一质量为m的小球以速度v0水平冲上小车，关于小球此后的运动情况，以下说法正确的是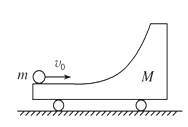
| A．小球可能从圆弧轨道上端抛出而不再回到小车 |
| B．小球可能离开小车水平向左做平抛运动 |
| C．小球可能离开小车做自由落体运动 |
| D．小球可能离开小车水平向右做平抛运动 |
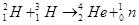.若
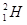和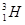
迎面碰撞，初速度大小分别为v1、v2. 
、
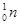的质量分别为m1、m2、m3、m4，反应后