题目内容
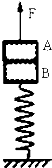 如图,A、B两个木块叠放在竖直轻弹簧上,mA=2kg,mB=1kg,轻弹簧的劲度系数为100N/m.在A上作用一个竖直向上的力F,使木块A由静止开始以2m/s2的加速竖直向上作匀加速运动,直到A、B分离时,弹簧的弹性势能减小了3.78J,g取10m/s2,则在这一匀加速运动的过程中有( )
如图,A、B两个木块叠放在竖直轻弹簧上,mA=2kg,mB=1kg,轻弹簧的劲度系数为100N/m.在A上作用一个竖直向上的力F,使木块A由静止开始以2m/s2的加速竖直向上作匀加速运动,直到A、B分离时,弹簧的弹性势能减小了3.78J,g取10m/s2,则在这一匀加速运动的过程中有( )| A、力F的最大值是24N | ||||
B、维持的时间是
| ||||
| C、A对B的压力做的功是-1.62J | ||||
| D、力F对木块做的功是2.7J |
分析:木块A受重力、B对A的支持力和拉力,要作匀加速运动,运用牛顿第二定律即可求解力F的最大值,根据胡克定律求出初始位置弹簧的压缩量和A、B分离时弹簧的压缩量,从而求出AB上升的高度,根据匀变速直线运动位移时间公式求解时间,分别以B及A、B整体作为研究对象,由动能定理求解A对B的压力做的功和力F对木块做的功.
解答:解:A、根据牛顿第二定律得:
F-mAg+FBA=mAa,
所以当FBA=0时,F最大,即
Fm=mAg+mAa=2×10×2×2=24 N,故A正确;
B、初始位置弹簧的压缩量x1=
=
=0.30m
A、B分离时,FBA=0,以B为研究对象可得:
FN-mBg=mBa,
FN=24N
此时x2=
=
=0.24m
A、B上升的高度:△x=x1-x2=0.30-0.24=0.06 m
根据△x=
at2得:
t=
=
=
s,故B错误;
C、A、B的速度v=
=
m/s
以B为研究对象,根据动能定理得:
mBv2=W弹-mBg△x+W压
解得:W压=-1.62J,故C正确;
D、以A、B作为一个整体,由动能定理得
WF+W弹-(mA+mB)g△x=
(mA+mB)v2
解得:WF=2.7J,故D正确.
故选:ACD
F-mAg+FBA=mAa,
所以当FBA=0时,F最大,即
Fm=mAg+mAa=2×10×2×2=24 N,故A正确;
B、初始位置弹簧的压缩量x1=
| mA+mB |
| k |
| 30 |
| 100 |
A、B分离时,FBA=0,以B为研究对象可得:
FN-mBg=mBa,
FN=24N
此时x2=
| FN |
| k |
| 24 |
| 100 |
A、B上升的高度:△x=x1-x2=0.30-0.24=0.06 m
根据△x=
| 1 |
| 2 |
t=
|
|
| ||
| 10 |
C、A、B的速度v=
| 2a△x |
| 0.24 |
以B为研究对象,根据动能定理得:
| 1 |
| 2 |
解得:W压=-1.62J,故C正确;
D、以A、B作为一个整体,由动能定理得
WF+W弹-(mA+mB)g△x=
| 1 |
| 2 |
解得:WF=2.7J,故D正确.
故选:ACD
点评:该题主要考查了牛顿第二定律的直接应用,要求同学们能正确分析物体的受力情况.动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.

练习册系列答案
相关题目
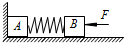 如图所示,在水平光滑地面上有A、B两个木块,A、B之间用一轻弹簧连接.A靠在墙壁上,用力F向左推B使两木块之间弹簧压缩并处于静止状态.若突然撤去力F,则下列说法中正确的是( )
如图所示,在水平光滑地面上有A、B两个木块,A、B之间用一轻弹簧连接.A靠在墙壁上,用力F向左推B使两木块之间弹簧压缩并处于静止状态.若突然撤去力F,则下列说法中正确的是( )| A、木块A离开墙壁前,墙对木块A的冲量大小等于木块B动量变化量的大小 | B、木块A离开墙壁前,弹性势能的减少量等于木块B动能的增量 | C、木块A离开墙壁时,B的动能等于A、B共速时的弹性势能 | D、木块A离开墙壁后,当弹簧再次恢复原长时,木块A的速度为零 |
 如图所示,A、B两个木块用轻弹簧相连接,它们静止在光滑水平面上,A和B的质量分别是99m和l00m,一颗质量为m的子弹以速度v0瞬间水平射入木块A内,并没有穿出.试求:
如图所示,A、B两个木块用轻弹簧相连接,它们静止在光滑水平面上,A和B的质量分别是99m和l00m,一颗质量为m的子弹以速度v0瞬间水平射入木块A内,并没有穿出.试求: 如图所示,质量分别为m和2m的A、B两个木块间用轻弹簧相连,放在光滑水平面上,A靠紧竖直墙.用水平力将B向左压,使弹簧被压缩一定长度,推到某位置静止时推力大小为F,弹簧的弹性势能为E.在此位置突然撤去推力,下列说法中正确的是( )
如图所示,质量分别为m和2m的A、B两个木块间用轻弹簧相连,放在光滑水平面上,A靠紧竖直墙.用水平力将B向左压,使弹簧被压缩一定长度,推到某位置静止时推力大小为F,弹簧的弹性势能为E.在此位置突然撤去推力,下列说法中正确的是( )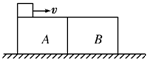 (1)在下列关于近代物理知识的说法中,正确的是
(1)在下列关于近代物理知识的说法中,正确的是