题目内容
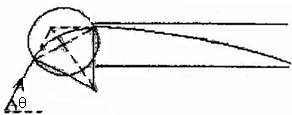
如图所示，纸平面内一带电粒子以某一速度做直线运动，一段时间后进入一垂直于纸面向里的圆形匀强磁场区域（图中未画出磁场区域），粒子飞出磁场后从上板边缘平行于板面进入两面平行的金属板间，两金属板带等量异种电荷，粒子在两板间经偏转后恰从下板右边缘飞出，已知带电粒子的质量为m，电量为q，其重力不计，粒子进入磁场前的速度方向与带电板成θ=60°角，匀强磁场的磁感应强度为B，带电板板长为l，板距为d，板间电压为U．试
（1）上金属板带什么电？
（2）粒子刚进入金属板时速度为多大？
（3）圆形磁场区域的最小面积为多大？
（1）上金属板带什么电？
（2）粒子刚进入金属板时速度为多大？
（3）圆形磁场区域的最小面积为多大？
（1）粒子在磁场中偏转的情况和左手定则可知，上金属板带负电．
（2）设带电粒子进入电场的初速度为v，在电场中偏转时有：
d=
at2=
(
)2 ①
解得：v=
②
（3）如图所示，带电粒子在磁场中所受洛伦兹力作为向心力，设磁偏转的半径为R，圆形磁场区域的半径为r，则：
qvB=m
③
得R=
=
④
由几何知识可得：r=Rsin30° ⑤
磁场区域的最小面积为S=πr2=
⑥
答：（1）上金属板带负电；
（2）粒子刚进入金属板时速度v=
；
（3）圆形磁场区域的最小面积为S=
．
（2）设带电粒子进入电场的初速度为v，在电场中偏转时有：
d=
| 1 |
| 2 |
| 1 |
| 2 |
| qU |
| dm |
| l |
| v |
解得：v=
| l |
| d |
|
（3）如图所示，带电粒子在磁场中所受洛伦兹力作为向心力，设磁偏转的半径为R，圆形磁场区域的半径为r，则：
qvB=m
| v2 |
| R |
得R=
| mv |
| qB |
| l |
| Bd |
|
由几何知识可得：r=Rsin30° ⑤
磁场区域的最小面积为S=πr2=
| πmUl2 |
| 8qB2d2 |
答：（1）上金属板带负电；
（2）粒子刚进入金属板时速度v=
| l |
| d |
|
（3）圆形磁场区域的最小面积为S=
| πmUl2 |
| 8qB2d2 |
练习册系列答案
相关题目
如图所示，纸平面内一带电粒子以某一速度做直线运动，一段时间后进入一垂直于纸面向里的圆形匀强磁场区域（图中未画出磁场区域），粒子飞出磁场后从上板边缘平行于板面进入两面平行的金属板间，两金属板带等量异种电荷，粒子在两板间经偏转后恰从下板右边缘飞出，已知带电粒子的质量为m，电量为q，其重力不计，粒子进入磁场前的速度方向与带电板成θ=60°角，匀强磁场的磁感应强度为B，带电板板长为l，板距为d，板间电压为U．试解答：
