题目内容
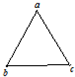 (2013?兰州模拟)匀强电场中有一等边三角形,a、b、c是它的三个顶点,电场方向与三角形所在平面平行.已知a、b和c点的电势分别为-
(2013?兰州模拟)匀强电场中有一等边三角形,a、b、c是它的三个顶点,电场方向与三角形所在平面平行.已知a、b和c点的电势分别为-| 3 |
| 3 |
分析:作出该三角形的外接圆,过c点作ab的垂线交ab于d点,已知a、b和c点的电势分别为-
V、
V和0V,则d点的电势也为0V,所以cd为0V等势面,则电场方向从高电势指向低电势且垂直于等势面,故电场方向从b指向a.过圆心O作ab的平行线ef交圆与ef两点,ef为沿电场方向上离OV的圆心最远的点,故e点的电势最低,f点的电势最高.根据几何关系计算Oe和Of的距离,再根据匀强电场的场强与电势差的关系U=Ed,计算e、f两点的电势.
| 3 |
| 3 |
解答:解: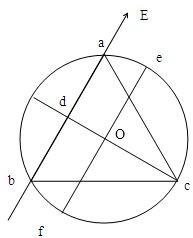 作出该三角形的外接圆,过c点作ab的垂线交ab于d点,已知a、b和c点的电势分别为-
作出该三角形的外接圆,过c点作ab的垂线交ab于d点,已知a、b和c点的电势分别为-
V、
V和0V,则d点的电势也为0V,所以cd为0V等势面,则电场方向从高电势指向低电势且垂直于等势面,故电场方向从b指向a,如图所示.过圆心O作ab的平行线ef交圆与ef两点,ef为沿电场方向上离OV的圆心最远的点,故e点的电势最低,f点的电势最高.
假设三角形的边长为dm,则根据电势差和场强的关系可知,电场强度为E=
=
=2
V/m.
根据几何关系可知,Oe的长度等于Of的长度等于外接圆的半径,等于
dm,
所以e点的电势为φ e=-UOe=-E?
d=-2
×
d=-2V,
f点的电势为φ f=UfO=E?
d=2
×
d=2V
即该三角形的外接圆上最低、最高电势分别为-2V和2V,
故B正确,ACD错误.
故选:B.
 作出该三角形的外接圆,过c点作ab的垂线交ab于d点,已知a、b和c点的电势分别为-
作出该三角形的外接圆,过c点作ab的垂线交ab于d点,已知a、b和c点的电势分别为-| 3 |
| 3 |
假设三角形的边长为dm,则根据电势差和场强的关系可知,电场强度为E=
| Uda | ||
|
| ||
|
| 3 |
| 1 |
| d |
根据几何关系可知,Oe的长度等于Of的长度等于外接圆的半径,等于
| ||
| 3 |
所以e点的电势为φ e=-UOe=-E?
| ||
| 3 |
| 3 |
| 1 |
| d |
| ||
| 3 |
f点的电势为φ f=UfO=E?
| ||
| 3 |
| 3 |
| 1 |
| d |
| ||
| 3 |
即该三角形的外接圆上最低、最高电势分别为-2V和2V,
故B正确,ACD错误.
故选:B.
点评:找等势点,作等势线,进一步作出电场线,并结合几何知识是求电势问题常用的方法.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 (2013?兰州模拟)如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( )
(2013?兰州模拟)如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( ) (2013?兰州模拟)如图所示,有一等腰直角三角形的区域,其斜边长为2L,高为L.在该区域内分布着如图所示的磁场,左侧小三角形内磁场方向垂直纸面向外,右侧小三角形内磁场方向垂直纸面向里,磁感应强度大小均为B.一边长为L、总电阻为R的正方形导线框abcd,从图示位置开始沿x轴正方向以速度v匀速穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则图乙中表示线框中电流i随bc边的位置坐标x变化的图象正确的是( )
(2013?兰州模拟)如图所示,有一等腰直角三角形的区域,其斜边长为2L,高为L.在该区域内分布着如图所示的磁场,左侧小三角形内磁场方向垂直纸面向外,右侧小三角形内磁场方向垂直纸面向里,磁感应强度大小均为B.一边长为L、总电阻为R的正方形导线框abcd,从图示位置开始沿x轴正方向以速度v匀速穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则图乙中表示线框中电流i随bc边的位置坐标x变化的图象正确的是( )