题目内容
3．美国宇航局发现了太阳系外第一颗类似地球的、可适合居住的行星--“开普勒-226”，其直径约为地球的2.4倍，至今其确切质量和表面成分仍不清楚．假设该行星的密度和地球相当．根据以上信息，估算该行星的第一宇宙速度为（ ）| A． | 3.3×103m/s | B． | 7.9×103m/s | C． | 1.2×104m/s | D． | 1.9×104m/s |
分析 根据万有引力提供向心力表示出第一宇宙速度．再根据已知的条件求解．
解答 解：第一宇宙速度是行星表面的运行速度，根据万有引力提供向心力得：$\frac{GMm}{{R}^{2}}$=$\frac{m{v}^{2}}{R}$
解得：v=$\sqrt{\frac{GM}{R}}$=$\sqrt{\frac{Gρ\frac{4}{3}π{R}^{3}}{R}}$
该行星的密度和地球相当，其直径约为地球的2.4倍．
所以该行星的第一宇宙速度是地球的第一宇宙速度的2.4倍．所以该行星的第一宇宙速度等于1.9×104m/s，
故选：D．
点评 求一个物理量之比，我们应该把这个物理量先用已知的物理量表示出来，再根据表达式进行比较．
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用．
练习册系列答案
相关题目
13．雨滴由静止开始下落（不计空气阻力），遇到水平方向吹来的风，设风对雨滴持续作用，下列说法中正确的是（ ）
| A． | 雨滴质量越大，下落时间将越短 | |
| B． | 雨滴下落时间与雨滴质量大小有关 | |
| C． | 同一雨滴风速越大，着地时动能越大 | |
| D． | 同一雨滴，着地时动能和风速无关 |
14．
近年来我国高速铁路发展迅速，现已知某新型国产机车总质量为m，如图已知两轨间宽度为L，内外轨高度差为h，重力加速度为g，如果机车要进入半径为R的弯道，请问，该弯道处的设计速度最为适宜的是（ ）
近年来我国高速铁路发展迅速，现已知某新型国产机车总质量为m，如图已知两轨间宽度为L，内外轨高度差为h，重力加速度为g，如果机车要进入半径为R的弯道，请问，该弯道处的设计速度最为适宜的是（ ）| A． | $\sqrt{\frac{gRh}{\sqrt{{L}^{2}-{h}^{2}}}}$ | B． | $\sqrt{\frac{gRh}{\sqrt{{L}^{2}-{R}^{2}}}}$ | C． | $\sqrt{\frac{gR\sqrt{{L}^{2}-{h}^{2}}}{h}}$ | D． | $\sqrt{\frac{gRL}{h}}$ |
11．
如图为一物体做匀变速直线运动的速度图象，在根据图象做出的以下判断中，正确的是（ ）
①物体始终沿正方向运动
②物体先沿负方向运动，在t=2s后物体开始沿正方向运动
③在t=2s前物体位于出发点负方向上，在t=2s后位于出发点正方向上
④在t=2s时，物体距出发点最远．
如图为一物体做匀变速直线运动的速度图象，在根据图象做出的以下判断中，正确的是（ ）①物体始终沿正方向运动
②物体先沿负方向运动，在t=2s后物体开始沿正方向运动
③在t=2s前物体位于出发点负方向上，在t=2s后位于出发点正方向上
④在t=2s时，物体距出发点最远．
| A． | ①② | B． | ③④ | C． | ②③ | D． | ②④ |
18．在做“研究匀变速直线运动”的实验中：
（1）实验室提供了以下器材：打点计时器、一端附有滑轮的长木板、小车、纸带、细绳、钩码、刻度尺、导线、交流电源、复写纸、弹簧测力计，其中在本实验中不需要的器材是弹簧测力计．
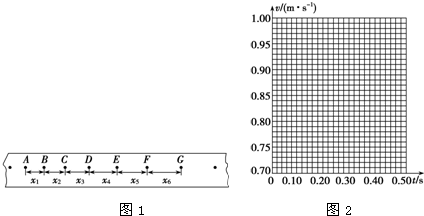
（2）如图1所示是某同学由打点计时器得到的表示小车运动过程的一条清晰纸带，纸带上两相邻计数点间还有四个点没有画出，打点计时器打点的时间间隔T=0.02s，其中x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.26cm．
如表列出了打点计时器打下B、C、F时小车的瞬时速度，请在表中填入打点计时器打下D、E两点的小车的瞬时速度．
（3）以A点为计时起点，在坐标图2中画出小车的速度-时间关系图线．
（4）根据你画出的小车的速度-时间关系图线计算出的小车的加速度a=0.64m/s2．
（1）实验室提供了以下器材：打点计时器、一端附有滑轮的长木板、小车、纸带、细绳、钩码、刻度尺、导线、交流电源、复写纸、弹簧测力计，其中在本实验中不需要的器材是弹簧测力计．
（2）如图1所示是某同学由打点计时器得到的表示小车运动过程的一条清晰纸带，纸带上两相邻计数点间还有四个点没有画出，打点计时器打点的时间间隔T=0.02s，其中x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.26cm．
如表列出了打点计时器打下B、C、F时小车的瞬时速度，请在表中填入打点计时器打下D、E两点的小车的瞬时速度．
| 位置 | B | C | D | E | F |
| 速度（m•s-1） | 0.737 | 0.801 | 0.994 |
（4）根据你画出的小车的速度-时间关系图线计算出的小车的加速度a=0.64m/s2．
质量为M、半径为R的质量分布均匀的球体，在正中央挖去半径为$\frac{R}{4}$的小球后，剩余的部分为阴影区域，如图所示．质量为m的质点P到球心O的距离为2R，引力常量为G．试求质点P受到的万有引力．（已知半径为R的球的体积公式为V=$\frac{4}{3}$πR3）
如图所示，一质量为m=0.5kg的小球，用长为l=0.4m的细线拴住在竖直面内作圆周运动．取g=10m/s2．试求：
如图所示，质量为mB=2kg的一端带有四分之一圆轨道的光滑平板车B，开始时静止在光滑水平面上，在平板车左端静止着一个质量为mA=2kg的物体A，一颗质量为m0=0.01kg的子弹以v0=500m/s的水平初速度瞬间射穿A后，速度变为v=100m/s，A在B上运动恰好能达到圆轨道最高点 （g=10m/s2）．求：
13．
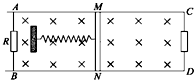如图所示，ABCD为固定的水平光滑矩形金属导轨，处在方向竖直向下，磁感应强度为B的匀强磁场中，AB间距为L，左右两端均接有阻值为R的电阻，质量为m、长为L且不计电阻的导体棒MN放在导轨上，与导轨接触良好，并与轻质弹簧组成弹簧振动系统．开始时，弹簧处于自然长度，导体棒MN具有水平向左的初速度v0，经过一段时间，导体棒MN第一次运动到最右端，这一过程中AB间R上产生的焦耳热为Q，则（ ）
如图所示，ABCD为固定的水平光滑矩形金属导轨，处在方向竖直向下，磁感应强度为B的匀强磁场中，AB间距为L，左右两端均接有阻值为R的电阻，质量为m、长为L且不计电阻的导体棒MN放在导轨上，与导轨接触良好，并与轻质弹簧组成弹簧振动系统．开始时，弹簧处于自然长度，导体棒MN具有水平向左的初速度v0，经过一段时间，导体棒MN第一次运动到最右端，这一过程中AB间R上产生的焦耳热为Q，则（ ）| A． | 初始时刻棒所受的安培力大小为$\frac{2{B}^{2}{L}^{2}{v}_{0}}{R}$ | |
| B． | 从初始时刻至棒第一次到达最左端的过程中，整个回路产生的焦耳热为$\frac{2Q}{3}$ | |
| C． | 当棒第一次到达最右端时，弹簧具有的弹性势能为$\frac{1}{2}$mv02-2Q | |
| D． | 当棒再一次回到初始位置时，AB间电阻的热功率为$\frac{{B}^{2}{L}^{2}{v}_{0}^{2}}{R}$ |