题目内容
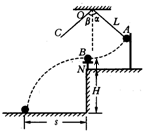
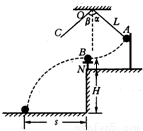
 用如图所示装置来探究碰撞中的守恒量,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,细线与竖直线之间夹角α;A球由静止释放,摆到最低点时恰与B球发生正碰,碰撞后,A球摆到与竖直夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸,用来记录球B的落点.
用如图所示装置来探究碰撞中的守恒量,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,细线与竖直线之间夹角α;A球由静止释放,摆到最低点时恰与B球发生正碰,碰撞后,A球摆到与竖直夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸,用来记录球B的落点.(1)用图中所示各个物理量的符号表示:碰撞前A球的速度VA=
(2)请你提供一条提高实验精度的建议:
分析:(1)根据机械能守恒定律求出A球碰前的速度;结合机械能守恒定律和平抛运动的规律分别求出碰后A、B两球的速度,根据动量守恒定律列出表达式.
(2)由于偶然误差,每次小球的落地点不同,可以采用多次测量取平均的方法得到落地点.
(2)由于偶然误差,每次小球的落地点不同,可以采用多次测量取平均的方法得到落地点.
解答:解:(1)A球下摆过程机械能守恒,根据机械能守恒定律得:
mAgl(1-cosα)=
m
解得:vA=
碰撞后B球做平抛运动,根据平抛运动的分位移公式,有:
水平方向:s=vBt
竖直方向:H=
gt2
解得:VB=s
碰撞后A球向上摆动过程机械能守恒,根据机械能守恒定律得:
-mBgl(1-cosβ)=-
m
解得:vA=
根据动量守恒定律,需验证:
mA
=mA
)+mBs
(2)由于偶然误差,每次小球的落地点不同,可以采用:多次测落点取平均值.
故答案为:(1)
,s
,mA
=mA
)+mBs
;(2)多次测落点取平均值.
mAgl(1-cosα)=
| 1 |
| 2 |
| v | 2 A |
解得:vA=
| 2gl(1-cosα) |
碰撞后B球做平抛运动,根据平抛运动的分位移公式,有:
水平方向:s=vBt
竖直方向:H=
| 1 |
| 2 |
解得:VB=s
|
碰撞后A球向上摆动过程机械能守恒,根据机械能守恒定律得:
-mBgl(1-cosβ)=-
| 1 |
| 2 |
| v | 2 B |
解得:vA=
| 2gl(1-cosβ) |
根据动量守恒定律,需验证:
mA
| 2gl(1-cosα) |
| 2gl(1-cosβ |
|
(2)由于偶然误差,每次小球的落地点不同,可以采用:多次测落点取平均值.
故答案为:(1)
| 2gl(1-cosα) |
|
| 2gl(1-cosα) |
| 2gl(1-cosβ |
|
点评:本题关键是明确实验原理,根据平抛运动的分位移公式和机械能守恒定律公式列式求解碰撞前后的速度,然后代入动量守恒定律公式进行验证.

练习册系列答案
相关题目
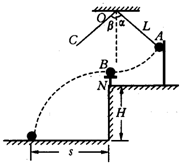
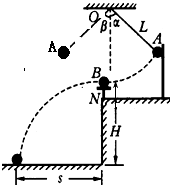
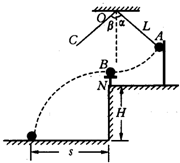 (2008?肇庆二模)(1)用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角α;球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,用来记录球B的落点.
(2008?肇庆二模)(1)用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角α;球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,用来记录球B的落点.