题目内容
【题目】如图所示，一带电量为+q、质量为m的小球，从距地面高2h处以一定的初速度水平抛出，在距抛出点水平距离为s处有根管口比小球大的竖直细管，细管的上口距地面高为h，为了使小球能无碰撞地落进管口通过管子，可在管子上方整个区域内加一水平向左的匀强电场，求：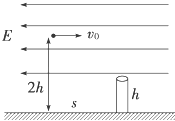
（1）小球的初速度；
（2）应加电场的场强；
（3）小球落地时的动能．
【答案】
（1）解：将小球的运动分解为水平方向和竖直方向，在竖直方向做自由落体运动，在水平方向上做匀减速直线运动到零，
小球运动至管上口的时间由竖直方向的运动决定：
h= 
t= 
水平方向，小球作匀减速运动，至管上口，水平方向速度为零，水平分位移：
S= 
t
解得：
v0=S 
答：小球的初速度为S ；
（2）解：水平方向，根据牛顿第二定律：qE=ma
又由运动学公式：
v0﹣ 
t=0，
由以上三式解得：
E= 
答：应加电场的场强为 ；
（3）解：由动能定理：WG+W电=△EK
即：Ek﹣ 
=mg（2h）﹣qES
解得：EK=2mgh
答：小球落地时的动能为2mgh．
【解析】（1）将小球的运动分解为水平方向和竖直方向，在竖直方向做自由落体运动，在水平方向上做匀减速直线运动，末速度为零，根据分运动合运动具有等时性求出水平初速度．（2）根据水平方向做匀减速直线运动根据速度位移公式求出运动的加速度，再根据牛顿第二定律求出电场强度．（3）小球落地的过程中有重力和电场力做功，根据动能定理求出小球落地的动能．
练习册系列答案
相关题目
