Question

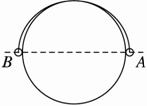
如图7-7-4所示，一个质量为m=0.2 kg的小球系于轻质弹簧的一端，且套在光滑竖直的圆环上，弹簧的上端固定于环的最高点A，环的半径R=0.5 m，弹簧的原长l₀=0.5 m，劲度系数为4.8 N/m.若小球从图示位置B点由静止开始滑动到最低点C时，弹簧的弹性势能E_p=0.6 J，求：(g取10 m/s²)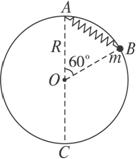

图7-7-4

(1)小球到C点时的速度v_C的大小；

(2)小球在C点对环的作用力.

Answer 1

解析：(1)小球在B点时弹簧处于原长，弹性势能为零.小球由B运动至C的过程，机械能守恒，则有

    mgR(1+cos60°)=E_p+mv_c²

    解得v_C=3 m/s.

(2)小球在C点时弹簧的弹力F=kx=k(2R-l₀)=2.4 N

    设环对球的作用力方向向下，大小为F_N，对小球由牛顿第二定律有

    F-mg-F_N=

    解得F_N=-3.2 N，负号说明环对球的作用力与规定的正方向相反，是向上的.由牛顿第三定律可知，小球对环的作用力的方向是向下的.

答案：(1)3 m/s  (2)3.2 N，方向向下