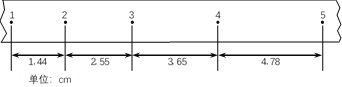
题目内容
【题目】平直路上向右运动的小车内,用细绳a和细绳b系住一个质量为3 kg的小球,细绳a与竖直方向夹角θ=37°,细绳b水平(如图所示),取g =10 m/s2.求:(已知:sin 37°=0.6,cos 37°=0.8)
(1)当小车作匀速直线运动时,两绳的拉力各为多少?
(2)假设小车向右运动过程中加速度![]() 从零逐渐增大,则要使b绳不松驰,则小车加速度最大不超过多少?
从零逐渐增大,则要使b绳不松驰,则小车加速度最大不超过多少?

【答案】(1)37.5N;22.5 N;(2)7.5 m/s2
【解析】
(1)小车匀速运动时,对小球受力分析,由物体的平衡条件有: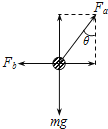
水平方向:
Fb-Fasin37°=0
竖直方向:
Facos37°-mg=0
代入数据解得:
Fa=37.5N
Fb=22.5N
(2)小车向右运动过程中加速度从零逐渐增大,b绳刚好不松弛时,Fb=0
对小球受力分析,由牛顿第二定律得:
F合=ma
![]()
解得:
a=gtanθ=10×0.75=7.5m/s2

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
【题目】如图所示是“探究弹力和弹簧伸长的关系”实验装置,小东认真操作、正确读数后得到的数据记录表如下。由表可知

次数 物理量 | 1 | 2 | 3 | 4 |
F/N | 0 | 0.98 | 1.96 | 2.94 |
l/cm | 12.0 | 14.0 | 16.0 | 18.0 |
x/cm | 0 | 2.0 | 4.0 | 6.0 |
A.每个钩码的质量为0.98 kgB.实验所用刻度尺的分度值是l mm
C.弹簧的劲度系数为49N/mD.弹簧的劲度系数随弹簧的拉力的增大而增大