题目内容
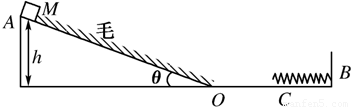
如图所示,物体在蒙有动物毛皮的斜面上运动.由于毛皮表面的特殊性,引起物体的运动有如下特点:①顺着毛的生长方向运动时毛皮产生的阻力可以忽略;②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力,且动摩擦因数μ恒定.斜面顶端距水平面高度为h=0.8m,质量为m=2kg的小物体M从斜面顶端A由静止滑下,从O点进入光滑水平滑道时无机械能损失,为使M制动,将轻弹簧的一端固定在水平滑道延长线B处的墙上,另一端恰位于水平轨道的中点C.已知斜面的倾角θ=53,动摩擦因数均为μ=0.5,其余各处的摩擦不计,g=10m/s2,下滑时逆着毛的生长方向,求:(1)弹簧压缩到最短时的弹性势能(设弹簧处于原长时弹性势能为零)
(2)若物块M能够被弹回到斜面上,则它能够上升的最大高度是多少?
(3)物块M在斜面上下滑过程中的总路程
【答案】分析:(1)物块M从斜面顶端A运动到弹簧压缩到最短,由动能定理求解弹簧压缩到最短时的弹性势能
(2)由动能定理研究上升的最大高度位置求解.
(3)物块M最终停止在水平面上,对于运动的全过程,由动能定理求解.
解答:解:(1)物块M从斜面顶端A运动到弹簧压缩到最短,由动能定理得
mgh-μmgcosθ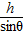 -Ep=0
-Ep=0
Ep=mgh-μmgcosθ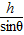 =10J
=10J
(2)设物块M第一次弹回,上升的最大高度为H,
由动能定理得:
mg(h-H)-μmgcos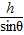 =0
=0
H=h-μgcos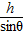 =0.5m
=0.5m
(3)物块M最终停止在水平面上,对于运动的全过程,由动能定理得
mgh-μmgcosθ?l=0
物块M在斜面上下滑过程中的总路程l=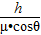 =2.67m
=2.67m
答:(1)弹簧压缩到最短时的弹性势能是10J
(2)若物块M能够被弹回到斜面上,则它能够上升的最大高度是0.5m
(3)物块M在斜面上下滑过程中的总路程是2.67m
点评:了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
一个题目可能需要选择不同的过程多次运用动能定理研究.
(2)由动能定理研究上升的最大高度位置求解.
(3)物块M最终停止在水平面上,对于运动的全过程,由动能定理求解.
解答:解:(1)物块M从斜面顶端A运动到弹簧压缩到最短,由动能定理得
mgh-μmgcosθ
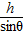 -Ep=0
-Ep=0Ep=mgh-μmgcosθ
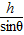 =10J
=10J(2)设物块M第一次弹回,上升的最大高度为H,
由动能定理得:
mg(h-H)-μmgcos
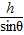 =0
=0H=h-μgcos
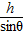 =0.5m
=0.5m(3)物块M最终停止在水平面上,对于运动的全过程,由动能定理得
mgh-μmgcosθ?l=0
物块M在斜面上下滑过程中的总路程l=
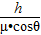 =2.67m
=2.67m答:(1)弹簧压缩到最短时的弹性势能是10J
(2)若物块M能够被弹回到斜面上,则它能够上升的最大高度是0.5m
(3)物块M在斜面上下滑过程中的总路程是2.67m
点评:了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
一个题目可能需要选择不同的过程多次运用动能定理研究.

练习册系列答案
相关题目
 (2010?山西模拟)如图所示,物体在蒙有动物毛皮的斜面上运动.由于毛皮表面的特殊性,引起物体的运动有如下特点:①顺着毛的生长方向运动时毛皮产生的阻力可以忽略;②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力.
(2010?山西模拟)如图所示,物体在蒙有动物毛皮的斜面上运动.由于毛皮表面的特殊性,引起物体的运动有如下特点:①顺着毛的生长方向运动时毛皮产生的阻力可以忽略;②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力.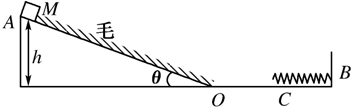

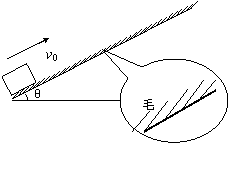 (2)一物体从斜面底端以初速v0=2m/s冲上足够长的斜面,斜面的倾斜角为q=30°,过了t=1.2s物体回到出发点。若认为毛皮产生滑动摩擦力时,动摩擦因数m为定值,g取10m/s2,则m的值为多少?
(2)一物体从斜面底端以初速v0=2m/s冲上足够长的斜面,斜面的倾斜角为q=30°,过了t=1.2s物体回到出发点。若认为毛皮产生滑动摩擦力时,动摩擦因数m为定值,g取10m/s2,则m的值为多少?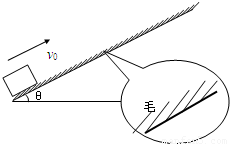 如图所示,物体在蒙有动物毛皮的斜面上运动.由于毛皮表面的特殊性,引起物体的运动有如下特点:①顺着毛的生长方向运动时毛皮产生的阻力可以忽略;②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力.
如图所示,物体在蒙有动物毛皮的斜面上运动.由于毛皮表面的特殊性,引起物体的运动有如下特点:①顺着毛的生长方向运动时毛皮产生的阻力可以忽略;②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力.