题目内容
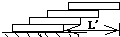 如图所示,四根完全一样的木条,长度均为L,叠放静止,则相对地面最大伸出量L′为
如图所示,四根完全一样的木条,长度均为L,叠放静止,则相对地面最大伸出量L′为
- A.L
- B.
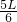
- C.
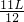
- D.
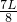
C
分析:每一块砖的质地均匀,厚度相同.分别以O1为支点、以O2为支点、以O3为支点时,支点右端的长度小于左端的长度,才不会向右翻倒.分别以O1为支点、以O2为支点、以O3为支点,列出不等式,解不等式即可.
解答:设上面的砖相对下面的砖伸出的长度分别为为x、y、z.如图.
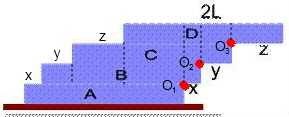 以O1为支点时,3x+2y+z<y+2z+3(L-x-y-z)…①
以O1为支点时,3x+2y+z<y+2z+3(L-x-y-z)…①
以O2为支点时,2y+z<z+2(L-y-z)…②
以O3为支点时,z<L-z…③
整理①②③得,
3x+2y+z<1.5L…④
2y+z<L…⑤
z<0.5L…⑥
④×2+⑤+⑥×3得:
6x+6y+6z<5.5L,
x+y+z< L.
L.
即L′<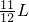
故选C
点评:本题是数学和物理结合的题目,有很大的难度,应该是一道竞赛题目.因为砖的质地均匀,厚度均匀,要使每一块砖不翻倒,只有支点右端的总长度小于左端的总长度即可.
分析:每一块砖的质地均匀,厚度相同.分别以O1为支点、以O2为支点、以O3为支点时,支点右端的长度小于左端的长度,才不会向右翻倒.分别以O1为支点、以O2为支点、以O3为支点,列出不等式,解不等式即可.
解答:设上面的砖相对下面的砖伸出的长度分别为为x、y、z.如图.
 以O1为支点时,3x+2y+z<y+2z+3(L-x-y-z)…①
以O1为支点时,3x+2y+z<y+2z+3(L-x-y-z)…①以O2为支点时,2y+z<z+2(L-y-z)…②
以O3为支点时,z<L-z…③
整理①②③得,
3x+2y+z<1.5L…④
2y+z<L…⑤
z<0.5L…⑥
④×2+⑤+⑥×3得:
6x+6y+6z<5.5L,
x+y+z<
 L.
L.即L′<
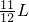
故选C
点评:本题是数学和物理结合的题目,有很大的难度,应该是一道竞赛题目.因为砖的质地均匀,厚度均匀,要使每一块砖不翻倒,只有支点右端的总长度小于左端的总长度即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,M、N是水平放置的一对正对平行金属板,其中M板中央有一小孔O,板间存在竖直向上的匀强电场,AB是一根长为9L的轻质绝缘细杆,在杆上等间距地固定着10个完全相同的带电小球,每个小球带电荷量为q,质量为m,相邻小球间的距离为L.现将最下端的小球置于O处,然后将AB由静止释放,AB在运动过程中始终保持竖直,经观察发现,在第四个小球进入电场到第五个小球进入电场前这一过程中,AB做匀速直线运动,求:
如图所示,M、N是水平放置的一对正对平行金属板,其中M板中央有一小孔O,板间存在竖直向上的匀强电场,AB是一根长为9L的轻质绝缘细杆,在杆上等间距地固定着10个完全相同的带电小球,每个小球带电荷量为q,质量为m,相邻小球间的距离为L.现将最下端的小球置于O处,然后将AB由静止释放,AB在运动过程中始终保持竖直,经观察发现,在第四个小球进入电场到第五个小球进入电场前这一过程中,AB做匀速直线运动,求: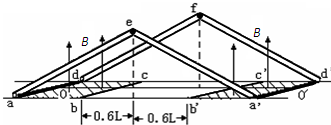

 +0.5t 的规律变化,取sin37°=0.6,cos37°=0.8。求:
+0.5t 的规律变化,取sin37°=0.6,cos37°=0.8。求: 
