题目内容
匀强电场的方向沿x轴正方向,电场强度E随x的分布如图所示,图中E0和d均为已知量.将带正电的质点A在O点由静止释放.A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放.当B在电场中运动时,A、B间的相互作用力及相互作用能均为零;B离开电场后,A、B间的相互作用视为静电作用.已知A的电荷量为Q,A和B的质量分别为m和 .不计重力.
.不计重力.
(1)求A在电场中的运动时间t;
(2)若B的电荷量为q= Q,求两质点相互作用能的最大值Epm;
Q,求两质点相互作用能的最大值Epm;
(3)为使B离开电场后不改变运动方向,求B所带电荷量的最大值qm.
(1) (2)Epm=
(2)Epm=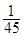 QE0d(3)qm=
QE0d(3)qm=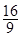 Q
Q
解析试题分析:(1)由牛顿第二定律,A在电场中运动的加速度a= =
=
A在电场中做匀变速直线运动 d= at2
at2
解得运动时间 t=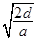 =
=
(2)设A、B离开电场时的速度分别为υA0、υB0,由动能定理,有
QE0d= m
m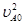 ,QE0d=
,QE0d=

 ①
①
A、B相互作用过程中,动量和能量守恒.A、B相互作用力为斥力,A受的力与其运动方向相同,B受的力与其运动方向相反,相互作用力对A做正功,对B做负功.A、B靠近的过程中,B的路程大于A的路程,由于相互作用力大小相等,相互作用力对B做功的绝对值大于对A做功的绝对值,因此相互作用力做功之和为负,相互作用能增加.所以,当A、B最接近时相互作用能最大,此时两者速度相同,设为υ′,有
(m+ )υ′= mυA0+
)υ′= mυA0+ υB0 ②
υB0 ②
Epm=( m
m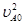 +
+

 )-
)- (m+
(m+ )υ′2 ③
)υ′2 ③
已知q = Q,由①、②、③式解得
Q,由①、②、③式解得
相互作用能的最大值 Epm=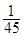 QE0d
QE0d
(3)考虑A、B在x>d区间的运动,由动量守恒、能量守恒,且在初态和末态均无相互作用,有
mυA+ υB= mυA0+
υB= mυA0+ υB0 ④
υB0 ④ m
m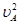 +
+

 =
= m
m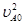 +
+

 ⑤ 由④、⑤解得 υB=-
⑤ 由④、⑤解得 υB=-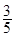 υB0+
υB0+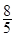 υA0
υA0
因B不改变运动方向,故 υB=-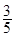 υB0+
υB0+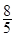 υA0 ≥0 ⑥
υA0 ≥0 ⑥
由①、⑥解得 q≤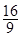 Q
Q
即B所带电荷量的最大值qm=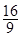 Q
Q
考点:考查了带电粒子在电场中的运动
点评::带电粒子在电场中的运动,综合了静电场和力学的知识,分析方法和力学的分析方法基本相同.先分析受力情况再分析运动状态和运动过程(平衡、加速、减速,直 线或曲线),然后选用恰当的规律解题.解决这类问题的基本方法有两种,第一种利用力和运动的观点,选用牛顿第二定律和运动学公式求解;第二种利用能量转化 的观点,选用动能定理和功能关系求解.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案 如图所示,在xoy平面内,匀强电场的方向沿x轴正向,匀强磁场的方向垂直于xoy平面向里.一电子在xoy平面内运动时,速度方向保持不变.则电子的运动方向沿( )
如图所示,在xoy平面内,匀强电场的方向沿x轴正向,匀强磁场的方向垂直于xoy平面向里.一电子在xoy平面内运动时,速度方向保持不变.则电子的运动方向沿( )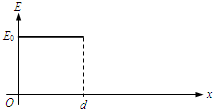 匀强电场的方向沿x轴正向,电场强度E随x的分布如图所示.图中E0和d均为已知量,将带正电的质点A在O点由能止释放,A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放,当B在电场中运动时,A、B间的相互作用力及相互作用能均为零;B离开电场后,A、B间的相作用视为静电作用,已知A的电荷量为Q,A和B的质量分别为m和
匀强电场的方向沿x轴正向,电场强度E随x的分布如图所示.图中E0和d均为已知量,将带正电的质点A在O点由能止释放,A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放,当B在电场中运动时,A、B间的相互作用力及相互作用能均为零;B离开电场后,A、B间的相作用视为静电作用,已知A的电荷量为Q,A和B的质量分别为m和
 .不计重力.
.不计重力. Q,求两质点相互作用能的最大值Epm;
Q,求两质点相互作用能的最大值Epm;