题目内容
长为L的细线一端固定于O点，如图所示，另一端拴一质量为m的小球．把小球拉至最高点A，以水平速度v0抛出．求当v0=
时，球运动到最低点C时细线的拉力大小．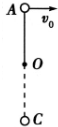
|
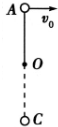
由于v0=
，小于小球做圆周运动通过最高点时的最小速度
，故小球做平抛运动，设小球运动到如图所示的B点时细线绷紧，此时细线与竖直方向的夹角为θ，由平抛运动规律有：Lsinθ=v0t；
L（1-cosθ）=
gt2
解得：θ=90°，说明B与O在同一直线上，vBx=
，由于细线瞬时绷紧，使小球水平速度突然变为零，所以此绷紧过程有机械能损失，然后小球以
的速度从B点开始做圆周运动到C点，由机械能守恒有：
mvBy2+mgL=
mvC2
在最低点C有：T-mg=
解得小球在最低点C时绳的拉力T=5mg．
|
| gL |
L（1-cosθ）=
| 1 |
| 2 |
解得：θ=90°，说明B与O在同一直线上，vBx=
|
| 2gL |
| 1 |
| 2 |
| 1 |
| 2 |
在最低点C有：T-mg=
m
| ||
| L |
解得小球在最低点C时绳的拉力T=5mg．
练习册系列答案
相关题目
一条长为L的细线一端固定在O点，另一端系着质量为m，带电量为-q的小球，整个装置处于足够大的水平方向的匀强电场中，静止于A点，此时细线与竖直方向成45°角，如图所示，现将小球沿圆周移动到O点的正止方B点，然后由静止释放．
（附加题） 长为L的细线一端固定一个带正电小球，另一端固定在O点，且处在一匀强电场中，小球受到的电场力等于其重力的
，小球才能通过A点
倍．当电场的取向合适时，可使小球在与水平方向成30°角的倾斜平面内做圆周运动，求此圆周运动的最大速度以及此时电场的方向．