题目内容
(附加题) 长为L的细线一端固定一个带正电小球,另一端固定在O点,且处在一匀强电场中,小球受到的电场力等于其重力的 倍.当电场的取向合适时,可使小球在与水平方向成30°角的倾斜平面内做圆周运动,求此圆周运动的最大速度以及此时电场的方向.
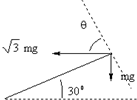
倍.当电场的取向合适时,可使小球在与水平方向成30°角的倾斜平面内做圆周运动,求此圆周运动的最大速度以及此时电场的方向.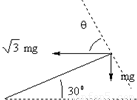
【答案】分析:据题,小球在与水平方向成30°角的倾斜平面内做圆周运动,在垂直于斜面平面内小球没有位移,合力为零,根据正交分解法求解电场力方向,判断电场强度方向.当小球位于斜面内最高点时,速度最小,由重力和电场力的合力提供向心力,由牛顿第二定律求出最小速度,根据动能定理求出最大速度.
解答:解: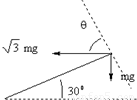 如图所示,小球在30°倾斜平面内作圆周运动时一定有:
如图所示,小球在30°倾斜平面内作圆周运动时一定有:
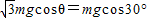
得θ=60°,因此电场力必沿水平向左方向,又因小球带正电,故电场方向也沿水平向左方向.
当速度最小时有: ,
,
得 ,
,
速度由最小到最大得过程中,由动能定理得:
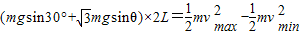
所以,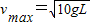
答:此圆周运动的最大速度为 .此时电场的方向为水平向左.
.此时电场的方向为水平向左.
点评:此题的突破口是小球倾斜平面内做圆周运动.小球速度最小的点称为物理的最高点,分析向心力的来源求出最小速度.
解答:解:
 如图所示,小球在30°倾斜平面内作圆周运动时一定有:
如图所示,小球在30°倾斜平面内作圆周运动时一定有: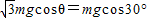
得θ=60°,因此电场力必沿水平向左方向,又因小球带正电,故电场方向也沿水平向左方向.
当速度最小时有:
 ,
,得
 ,
,速度由最小到最大得过程中,由动能定理得:
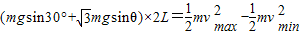
所以,
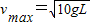
答:此圆周运动的最大速度为
 .此时电场的方向为水平向左.
.此时电场的方向为水平向左.点评:此题的突破口是小球倾斜平面内做圆周运动.小球速度最小的点称为物理的最高点,分析向心力的来源求出最小速度.

练习册系列答案
相关题目
 (附加题)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计电子所受重力).
(附加题)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计电子所受重力). (附加题) 长为L的细线一端固定一个带正电小球,另一端固定在O点,且处在一匀强电场中,小球受到的电场力等于其重力的
(附加题) 长为L的细线一端固定一个带正电小球,另一端固定在O点,且处在一匀强电场中,小球受到的电场力等于其重力的