题目内容
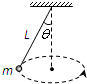 如图,小球做匀速圆周运动,细线与竖直方向夹角为θ,线长为L,小球质量为m,重力加速度为g.求:
如图,小球做匀速圆周运动,细线与竖直方向夹角为θ,线长为L,小球质量为m,重力加速度为g.求:(1)绳子对小球的拉力的大小;
(2)小球运动的向心加速度大小;
(3)小球运动的周期.
分析:(1)小球做匀速圆周运动,由合外力提供向心力.先对小球进行运动分析,做匀速圆周运动,再找出合力的方向,进一步求绳子对小球的拉力的大小.
(2)根据合外力提供向心力,列式求解小球运动的向心加速度大小;
(3)由向心加速度公式a=
r,r=Lsinθ,求解周期.
(2)根据合外力提供向心力,列式求解小球运动的向心加速度大小;
(3)由向心加速度公式a=
| 4π2 |
| T2 |
解答:解:(1)小球在水平面内做匀速圆周运动,对小球受力分析,小球的合力提供向心力,如图,
则得:T=
;
 (2)根据牛顿第二定律得:mgtanθ=ma,得:a=gtanθ.
(2)根据牛顿第二定律得:mgtanθ=ma,得:a=gtanθ.
(3)由向心加速度公式a=
r,r=Lsinθ,解得 T=2π
.
答:(1)绳子对小球的拉力的大小为
;
(2)小球运动的向心加速度大小为gtanθ;
(3)小球运动的周期为2π
.
则得:T=
| mg |
| cosθ |
 (2)根据牛顿第二定律得:mgtanθ=ma,得:a=gtanθ.
(2)根据牛顿第二定律得:mgtanθ=ma,得:a=gtanθ.(3)由向心加速度公式a=
| 4π2 |
| T2 |
|
答:(1)绳子对小球的拉力的大小为
| mg |
| cosθ |
(2)小球运动的向心加速度大小为gtanθ;
(3)小球运动的周期为2π
|
点评:向心力是效果力,匀速圆周运动中由合外力提供,作出受力图,运用牛顿第二定律进行求解.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,求:
在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,求: 如图所示,两根长度不同的细线分别系有两个小球,细线的上端都系于O点.设法让两个小球在同一水平面上做匀速圆周运动.已知细线长之比为L1:L2=
如图所示,两根长度不同的细线分别系有两个小球,细线的上端都系于O点.设法让两个小球在同一水平面上做匀速圆周运动.已知细线长之比为L1:L2=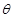 ,线长为L,小球质量为m,重力加速度为g.求:(1)绳子对小球的拉力的大小;
,线长为L,小球质量为m,重力加速度为g.求:(1)绳子对小球的拉力的大小;
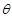 ,线长为L,小球质量为m,重力加速度为g.求:(1)绳子对小球的拉力的大小;
,线长为L,小球质量为m,重力加速度为g.求:(1)绳子对小球的拉力的大小;