题目内容
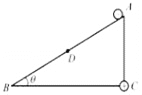
【题目】如图所示，倾角为θ=30°的光滑绝缘直角斜面ABC，D是斜边AB的中心，在C点固定一个带电荷量为+Q的点电荷．一质量为m，电荷量为﹣q的小球从A点由静止释放，小球经过D点时的速度为v，到达B点时的速度为0，则（ ）
A. 小球从A到D的过程中静电力做功为
mv2
B. 小球从A到D的过程中电势能逐渐减小
C. 小球从A到B的过程中电势能先减小后增加
D. AB两点间的电势差UAB=
【答案】CD
【解析】
根据动能定理研究该质点从A点滑到非常接近斜边底端B点的过程，其中的A、D点是同一等势面上，然后结合动能定理即可判断．
A.斜面的倾角为
，斜面上
，由几何关系可知，
，即A到C的距离与D到C的距离是相等的，所以D与A的电势相等，则由
，知A到D的过程中电场力做的功等于0，A错误；由于即A到C的距离与D到C的距离是相等的，由几何关系可知，沿AD的方向上的各点到C的距离先减小后增大，距离减小的过程中电场力对负电荷做正功，所以从A到D的过程中负电荷的电势能先减小后增大，B错误；结合B的分析，同理可知，小球从A到B的过程中电势能先减小后增加，C正确；设AB的长度为2L，则
，在小球从A到D两点得过程中，由动能定理有：
，在小球从A到B的过程中有：
，所以：
，D正确．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
