题目内容
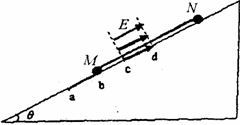
 如图19所示,小球N带电+q,小球M不带
如图19所示,小球N带电+q,小球M不带
电,两球质量均为m,用一根长4L的绝缘轻
质细杆连接,放在一个倾角为θ的足够长绝
缘斜面上.斜面ab部分粗糙,且小球与斜面
间的动摩擦因数为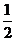 tanθ,其它部分光滑,
tanθ,其它部分光滑,
cd段有一平行斜面向上的有界匀强电场.已
知ab=bc=cd=L,重力加速度为g.现让两球从如图所示位置(即M球在b点)由静
止释放,两小球向下运动,当N球到达c点时恰好开始返回.(两球均可视为质点)求:
(1)匀强电场的场强E的大小;
(2)释放后球M第一次沿斜面向上运动的最高点到a点的距离.
【答案】
解:(1)设匀强电场的场强为E,
2mg×3Lsinθ-μmgLcosθ-EqL=(5分)
∴E=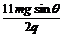 (1分)
(1分)
(2)由题意知,M点第一次向上运动,所能到达的最高点位于a、b之间,设该点距a点的距离为x,对M、N从由静止释放到球M第一次沿斜面向上运动到最高点的过程中,由动能定理得:
2mg(L-x)sinθ-μmg(L+x)cosθ=(5分)
∴x=0.6L(1分)

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目



 =
= 

































 g
g
 。
。





