题目内容
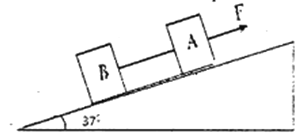
【题目】如图所示,质量均为1kg的A、B两物块置于倾角为37°斜面上,物块与地面间的动摩擦因数均为![]() ,物块间用一与斜面平行的轻绳相连,绳中无拉力现用力F沿斜面向上拉物块A,假设最大静摩擦力等于滑动摩擦力。重力加速度为g。下列说法中正确的是
,物块间用一与斜面平行的轻绳相连,绳中无拉力现用力F沿斜面向上拉物块A,假设最大静摩擦力等于滑动摩擦力。重力加速度为g。下列说法中正确的是
A. 当0<F≤12N时,绳中拉力为0
B. 当F=2N时,A物块摩擦力5N
C. 当F>24N时,绳中拉力为![]()
D. 当F=20N时,B物块摩擦力4N
【答案】AC
【解析】
A、mgsin37°=μmgcos37°=6N,当0<F≤mgsin37°+μmgcos37°=12N时,沿斜面方向,A受到拉力、重力分力与静摩擦力的作用,三者可以平衡,绳中拉力为0,故A正确;
B、当F=2N时,A物块摩擦力向上,大小f=mgsin37°-F=4N,故B错误;
C. 当F>2mgsin37°+2μmgcos37°=24N时,整体向上加速运动,根据牛顿第二定律,设绳子拉力为T:
对整体:F-2mgsin37°-2μmgcos37°=2ma
对B:T- mgsin37°-μmgcos37°=ma
可得,绳中拉力为![]() ,故C正确;
,故C正确;
D. 当F=20N时,整体不动。设绳子拉力为T:
对A:F=T+mgsin37°+μmgcos37°,T=8N
对B:T=mgsin37°+f,f=2N,故B错误。
故选:AC

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目