题目内容

精英家教网如图所示，在某空间实验室中，有两个靠在一起的等大的圆柱体区域，分别存在着等大反向的匀强磁场，磁感应强度B=0.10T，磁场区域半径r=
2
3
3
m，左侧区圆心为O1，磁场向里，右侧区圆心为O2，磁场向外，两区域切点为C．今有质量m=3.2×10-26kg，带电量q=-1.6×10-19C的某种粒子，从左侧区边缘的A点以速度v=1.0×106m/s沿正对O1的方向垂直射入磁场，结果它恰好穿越C点后再从右侧区穿出．求：该粒子通过两磁场区域所用的时间（结果保留三位有效数字）
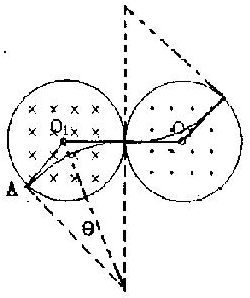
分析：粒子从A点进入匀强磁场后，由洛伦兹力提供向心力，做匀速圆周运动，根据牛顿第二定律求出轨迹半径，得出轨迹的圆心角，由运动时间与周期的关系求出粒子从A到C的时间．粒子穿越右侧磁场的时间与穿越左侧磁场的时间相等，再求解总时间．
解答：解：该离子在磁场中做匀速圆周运动，其运动轨迹如图所示，设轨迹半径为R，圆周运动的周期为T．由牛顿第二定律有
    qvB=m
v2
R
   得到  R=
mv
qB
精英家教网
运动周期  T=
2πR
v
=
2πm
qB

代入解得   R=2m
由数学知识得到
    tanθ=
r
R
=
3
3
，θ=30°
则该粒子通过两磁场区域所用的时间t=2×
2θ
360°

代入解得
   t=4.19×10-6s
答：该粒子通过两磁场区域所用的时间是4.19×10-6s．
点评：本题是有界磁场问题，关键是画出粒子的运动轨迹，运用几何知识求解半径．
练习册系列答案
相关题目
某同学设想用带电粒子的运动轨迹做出“0”字样，首先，在真空空间的竖直平面内建立xoy坐标系，在x1=-0.1m和x2=0.1m处有两个与y轴平行的竖直界面PQ、MN把空间分成Ⅲ、Ⅱ、Ⅰ三个区域，在这三个区域中分别存在匀强磁场B3、B2、B1，其大小满足B2=2B3=2B1=0.02T，方向如图所示．在Ⅱ区域中的x轴上、下两侧还分别存在匀强电场E1、E2（图中未画出），忽略所有电、磁场的边缘效应，ABCD是以坐标原点O为中心对称的正方形，其边长a=0.2m．现在界面MN上的A点沿x轴正方向发射一个比荷q/m=1.0×108C/kg的带正电的粒子（其重力不计），粒子恰能沿图中实线运动，途经B、C、D三点后回到A点，做周期性运动，轨迹构成一个“0”字，已知粒子每次穿越Ⅱ区域时均作直线运动．试求：

（1）粒子自A点射出时的速度大小v0；
（2）电场强度E1、E2的大小和方向；
（3）粒子作一次周期性运动所需的时间．
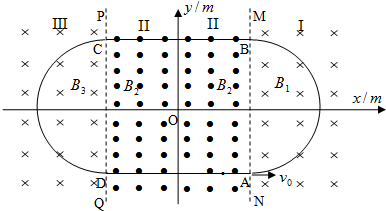
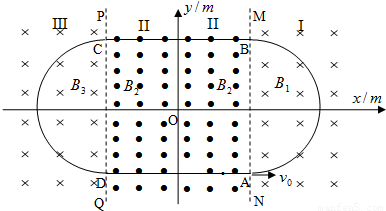
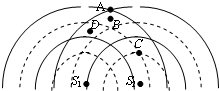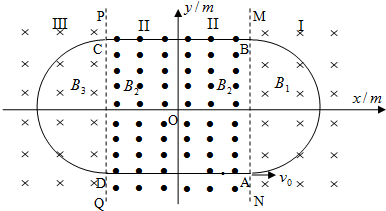
如图所示，S1、S2是两个频率相同的波源，它们发出的两列简谐横波在空间相遇，图中虚线和实线分别代表某时刻这两列波的波谷和波峰，则下列说法中正确的是（　　）
（2009?日照一模）某同学设想用带电粒子的运动轨迹做出“0”、“8”字样，首先，如图甲所示，在真空空间的竖直平面内建立．roy坐标系，在y1=0.1m和y2=一0.1m处有两个与z轴平行的水平界面PQ和MN把空间分成I、Ⅱ、Ⅲ三个区域，在三个区域中分别存在匀强磁场B1、B2、B3其大小满足B=2=B1=2B3=0.02T，方向如图甲所示．在Ⅱ区域中的y轴左右两侧还分别存在匀强电场E1、E2（图中未画出），忽略所有电、磁场的边缘效应．ABCD是以坐标原点．为中心对称的正方形，其边长L=0.2m．现在界面PQ上的A处沿y轴正方向发射一比荷
qm
=108C/kg的带正电荷的粒子（其重力不计），粒子恰能沿图中实线途经BCD三点后回到A点并做周期性运动，轨迹构
成一个“0”字．已知粒子每次穿越Ⅱ区域时均做直线运动．
（1）求电场E1、E2的大小和方向．
（2）去掉Ⅱ和Ⅲ区域中的匀强电场和磁场，其他条件不变，仍在A处以相同的速度发射相同的粒子，使粒子运动的轨迹成为上、下对称的“8”字，且运动周期不变，请在答题纸中的乙图上Ⅱ和Ⅲ区域内重新设计适当的匀强电场或匀强磁场，并画出带电粒子的运动轨迹和你所设计的“场”．
某同学设想用带电粒子的运动轨迹做出“0”字样，首先，在真空空间的竖直平面内建立xoy坐标系，在x1=-0.1m和x2=0.1m处有两个与y轴平行的竖直界面PQ、MN把空间分成Ⅲ、Ⅱ、Ⅰ三个区域，在这三个区域中分别存在匀强磁场B3、B2、B1，其大小满足B2=2B3=2B1=0.02T，方向如图所示．在Ⅱ区域中的x轴上、下两侧还分别存在匀强电场E1、E2（图中未画出），忽略所有电、磁场的边缘效应，ABCD是以坐标原点O为中心对称的正方形，其边长a=0.2m．现在界面MN上的A点沿x轴正方向发射一个比荷q/m=1.0×108C/kg的带正电的粒子（其重力不计），粒子恰能沿图中实线运动，途经B、C、D三点后回到A点，做周期性运动，轨迹构成一个“0”字，已知粒子每次穿越Ⅱ区域时均作直线运动．试求：

精英家教网

（1）粒子自A点射出时的速度大小v0；
（2）电场强度E1、E2的大小和方向；
（3）粒子作一次周期性运动所需的时间．
某同学设想用带电粒子的运动轨迹做出“0”字样，首先，在真空空间的竖直平面内建立xoy坐标系，在x1=-0.1m和x2=0.1m处有两个与y轴平行的竖直界面PQ、MN把空间分成Ⅲ、Ⅱ、Ⅰ三个区域，在这三个区域中分别存在匀强磁场B3、B2、B1，其大小满足B2=2B3=2B1=0.02T，方向如图所示．在Ⅱ区域中的x轴上、下两侧还分别存在匀强电场E1、E2（图中未画出），忽略所有电、磁场的边缘效应，ABCD是以坐标原点O为中心对称的正方形，其边长a=0.2m．现在界面MN上的A点沿x轴正方向发射一个比荷q/m=1.0×108C/kg的带正电的粒子（其重力不计），粒子恰能沿图中实线运动，途经B、C、D三点后回到A点，做周期性运动，轨迹构成一个“0”字，已知粒子每次穿越Ⅱ区域时均作直线运动．试求：

（1）粒子自A点射出时的速度大小v；
（2）电场强度E1、E2的大小和方向；
（3）粒子作一次周期性运动所需的时间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网