题目内容
 如图,水平放置的金属薄板A、B间有匀强电场,已知B板电势高于A板.电场强度E=5×105N/C,间距d=1.25m.A板上有一小孔,M恰好在孔的正上方,距离h=1.25m.从M处每隔相等时间间隔由静止释放一个质量m=1×10-3kg的带电小球.第1个带电小球的电量q1=+1×10-8C,第n个带电小球的电量qn=nq1.取g=10m/s2.求:
如图,水平放置的金属薄板A、B间有匀强电场,已知B板电势高于A板.电场强度E=5×105N/C,间距d=1.25m.A板上有一小孔,M恰好在孔的正上方,距离h=1.25m.从M处每隔相等时间间隔由静止释放一个质量m=1×10-3kg的带电小球.第1个带电小球的电量q1=+1×10-8C,第n个带电小球的电量qn=nq1.取g=10m/s2.求:(1)第1个带电小球从M下落至B板的时间;
(2)第几个带电小球将不能抵达B板;
(3)第(2)问中该带电小球下落过程中机械能的变化量.
分析:(1)小球先做自由落体运动,由运动学位移公式求出自由下落到小孔的时间,由位移速度公式求出到达A板小孔的速度.小球在匀强电场中做匀加速运动,根据牛顿第二定律和运动学位移公式结合时间,即可得到总时间.
(2)随着小球电量的增大,进入电场的小球会做匀减速运动,当小球刚好到达B板的速度为零时,根据动能定理求出这个小球的电量,即可根据条件:qn=nq1求解.
(3)由上题的结果,结合机械能的变化量等于电场力做功,由功能关系求解.
(2)随着小球电量的增大,进入电场的小球会做匀减速运动,当小球刚好到达B板的速度为零时,根据动能定理求出这个小球的电量,即可根据条件:qn=nq1求解.
(3)由上题的结果,结合机械能的变化量等于电场力做功,由功能关系求解.
解答:解:(1)对于小球自由下落的过程,有 h=
g
解得,t1=
=
s=0.5s;
小球到达小孔时的速度为 v1=
=
m/s=5m/s;
小球在匀强电场中的加速度 α1=
=g-
=10-
=5m/s2;
由d=v1t2+
a1t22得:
2t22+4t2-1=0,
解得:t2=
s≈0.22s.
故第1个带电小球从M下落至B板的时间为 t=t1+t2=0.5s+0.22s=0.72s
(2)对第n小球,对全过程运用动能定理得:mg(h+d)-Eqnd=△Ek=0,
得 qn=
=
C=4×10-8C,
则 n=
=4,即第4个小球恰好抵达B板,则第5个小球不能到达B板;
(3)对第5小球,设进入电场的深度为x.
根据动能定理得:mg(h+x)-Eq5x=△Ek=0,
解得 x=
m,
所以机械能的变化量为△E机=-mg(h+x)=-Eq5x=5×105×5×10-8×
=-
×10-2J=-2.08×10-2J.
答:(1)第1个带电小球从M下落至B板的时间为0.72s;
(2)第5个带电小球将不能抵达B板;
(3)第(2)问中该带电小球下落过程中机械能的变化量为-2.08×10-2J.
| 1 |
| 2 |
| t | 2 1 |
解得,t1=
|
|
小球到达小孔时的速度为 v1=
| 2gh |
| 2×10×1.25 |
小球在匀强电场中的加速度 α1=
| mg-Eq |
| m |
| Eq |
| m |
| 5×105×10-8 |
| 1×10-3 |
由d=v1t2+
| 1 |
| 2 |
2t22+4t2-1=0,
解得:t2=
| ||
| 2 |
故第1个带电小球从M下落至B板的时间为 t=t1+t2=0.5s+0.22s=0.72s
(2)对第n小球,对全过程运用动能定理得:mg(h+d)-Eqnd=△Ek=0,
得 qn=
| mg(h+d) |
| Ed |
| 1×10-3×10×2.5 |
| 5×105×1.25 |
则 n=
| qn |
| q1 |
(3)对第5小球,设进入电场的深度为x.
根据动能定理得:mg(h+x)-Eq5x=△Ek=0,
解得 x=
| 5 |
| 6 |
所以机械能的变化量为△E机=-mg(h+x)=-Eq5x=5×105×5×10-8×
| 5 |
| 6 |
| 25 |
| 12 |
答:(1)第1个带电小球从M下落至B板的时间为0.72s;
(2)第5个带电小球将不能抵达B板;
(3)第(2)问中该带电小球下落过程中机械能的变化量为-2.08×10-2J.
点评:本题两个过程的问题,分段运用力学方法处理是常用的方法,对于动能定理也可以运用全程法研究.

练习册系列答案
相关题目
 如图,水平放置的金属导轨M、N,平行地置于匀强磁场中,间距为d,磁场的磁感强度大小为B,方向竖直向上,金属棒ab的质量为m,放在导轨上且与导轨垂直.已知导轨与金属棒间的动摩擦因数为μ(最大静摩擦力与滑动摩擦力相等),电源电动势为E,定值电阻为R,其余部分电阻不计.电键K闭合后,金属将开始运动,则当电键K闭合的瞬间,棒ab的加速度为多大?
如图,水平放置的金属导轨M、N,平行地置于匀强磁场中,间距为d,磁场的磁感强度大小为B,方向竖直向上,金属棒ab的质量为m,放在导轨上且与导轨垂直.已知导轨与金属棒间的动摩擦因数为μ(最大静摩擦力与滑动摩擦力相等),电源电动势为E,定值电阻为R,其余部分电阻不计.电键K闭合后,金属将开始运动,则当电键K闭合的瞬间,棒ab的加速度为多大? 如图,水平放置的金属导轨平行地置于匀强磁场中,间距为L=1m,磁场的磁感强度大小为B=1T,方向与导轨平面夹为α=37°,电源电动势为E=3V,定值电阻R=15Ω,其余部分电阻不计.金属棒ab的质量为1kg,始终静止在导轨上且与导轨垂直.(sin37°=0.6,cos 37°=0.8,取g=10m/s2)
如图,水平放置的金属导轨平行地置于匀强磁场中,间距为L=1m,磁场的磁感强度大小为B=1T,方向与导轨平面夹为α=37°,电源电动势为E=3V,定值电阻R=15Ω,其余部分电阻不计.金属棒ab的质量为1kg,始终静止在导轨上且与导轨垂直.(sin37°=0.6,cos 37°=0.8,取g=10m/s2) 如图,水平放置的金属薄板A、B间有匀强电场,电场强度大小E=2.0×106N/C.A板上有一小孔,D为小孔正上方h=3.2cm处的一点.一带负电的油滴在重力G=3.2×10-12N作用下,由D点静止开始做自由落体运动.当油滴进入电场后,恰好做匀速直线运动.求:(g取10m/s2)
如图,水平放置的金属薄板A、B间有匀强电场,电场强度大小E=2.0×106N/C.A板上有一小孔,D为小孔正上方h=3.2cm处的一点.一带负电的油滴在重力G=3.2×10-12N作用下,由D点静止开始做自由落体运动.当油滴进入电场后,恰好做匀速直线运动.求:(g取10m/s2)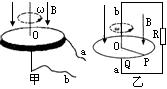 圆盘发电机的构造如图甲水平放置的金属圆盘在竖直向下的匀强磁场中绕与圆盘平面垂直且过圆盘中心O点的轴匀速转动,从a、b两端将有电压输出。现将此发电机简化成如图乙所示的模型:固定的金属圆环水平放置,金属棒OP绕圆环中心O以角速度
圆盘发电机的构造如图甲水平放置的金属圆盘在竖直向下的匀强磁场中绕与圆盘平面垂直且过圆盘中心O点的轴匀速转动,从a、b两端将有电压输出。现将此发电机简化成如图乙所示的模型:固定的金属圆环水平放置,金属棒OP绕圆环中心O以角速度